Infinite Geometric Series
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 8 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Answered
- Review
-
Question 1 of 8
1. Question
A kangaroo slows down its jumping as it approaches a lake.
Starting at `6`m, its next jump covers half of the previous jump. Find the limiting sum of the distances that the kangaroo jumps over.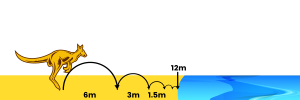
- `S_∞=` (12)` \text(m)`
Hint
Help VideoCorrect
Great Work!
Incorrect
Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`Common Ratio Formula
$$\color{#00880A}{r}=\frac{U_2}{U_1}=\frac{U_3}{U_2}$$First, solve for the value of `r`.$$\color{#00880A}{r}$$ `=` $$\frac{U_2}{U_1}$$ `=` $$\frac{3}{6}$$ Substitute the first and second term `=` `1/2` Simplify Next, substitute the known values to the formula`\text(First term)``[a]` `=` `6` `\text(Common Ratio)``[r]` `=` `1/2` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{6}}{1-\color{#00880A}{\frac{1}{2}}}$$ Substitute known values `=` `6/(1/2)` Evaluate `=` `12` `S_∞=12 \text(m)` -
Question 2 of 8
2. Question
Find the limiting sum`1-1/3+1/9-1/27…`Write fractions as “a/b”- `S_∞=` (3/4)
Hint
Help VideoCorrect
Excellent!
Incorrect
Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`Common Ratio Formula
$$\color{#00880A}{r}=\frac{U_2}{U_1}=\frac{U_3}{U_2}$$First, solve for the value of `r`.$$\color{#00880A}{r}$$ `=` $$\frac{U_2}{U_1}$$ `=` $$\frac{-\frac{1}{3}}{1}$$ Substitute the first and second term `=` `-1/3` Next, substitute the known values to the formula`\text(First term)``[a]` `=` `1` `\text(Common Ratio)``[r]` `=` `-1/3` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{1}}{1-\left(\color{#00880A}{-\frac{1}{3}}\right)}$$ Substitute known values `=` `1/(4/3)` Evaluate `=` `3/4` `S_∞=3/4` -
Question 3 of 8
3. Question
Find the value of `r` given that:`S_∞=18``U_1=6`Write fractions as “a/b”- `r=` (2/3)
Hint
Help VideoCorrect
Nice Job!
Incorrect
Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`Substitute the known values then solve for `r``S_∞` `=` `18` `\text(1st term)` `=` `6` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ $$\color{#9a00c7}{18}$$ `=` $$\frac{\color{#e65021}{6}}{1-\color{#00880A}{r}}$$ Substitute known values `18(1-r)` `=` `6` Cross multiply `18-18r` `=` `6` Distribute `18-18r` `-18` `=` `6` `-18` Subtract `18` from both sides `-18r` `divide(-18)` `=` `-12` `divide(-18)` Divide both sides by `-18` `r` `=` `12/18` `r` `=` `2/3` Simplify `r=2/3` -
Question 4 of 8
4. Question
Given that `S_∞=4/5`, find the value of `x``x+x^2+x^3…`Write fractions as “a/b”- `x=` (4/9)
Hint
Help VideoCorrect
Well Done!
Incorrect
Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`Common Ratio Formula
$$\color{#00880A}{r}=\frac{U_2}{U_1}=\frac{U_3}{U_2}$$First, solve for the value of `r`.$$\color{#00880A}{r}$$ `=` $$\frac{U_2}{U_1}$$ `=` $$\frac{x^2}{x}$$ Substitute the first and second term `=` `x` Next, substitute the known values then solve for `x``S_∞` `=` `4/5` `\text(First term)``[a]` `=` `x` `\text(Common Ratio)``[r]` `=` `x` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ $$\color{#9a00c7}{\frac{4}{5}}$$ `=` $$\frac{\color{#e65021}{x}}{1-\color{#00880A}{x}}$$ Substitute known values `4(1-x)` `=` `5x` Cross multiply `4-4x` `=` `5x` Distribute `4-4x` `+4x` `=` `5x` `+4x` Add `4x` to both sides `4``divide9` `=` `9x``divide9` Divide both sides by `9` `4/9` `=` `x` `x` `=` `4/9` `x=4/9` -
Question 5 of 8
5. Question
An acrobatic stunt plane flies vertically upwards. The further it goes up, the more it allows gravity to take over its flight, slowing it down until it reaches a peak point. At the first second, it travels `120`m, `40`m at the next, then `13 1/3`m, and so on. Find the total distance that the plane travels upwards until reaching the peak point.- `S_∞=` (180)` \text(m)`
Hint
Help VideoCorrect
Correct!
Incorrect
Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`Common Ratio Formula
$$\color{#00880A}{r}=\frac{U_2}{U_1}=\frac{U_3}{U_2}$$First, solve for the value of `r`.$$\color{#00880A}{r}$$ `=` $$\frac{U_2}{U_1}$$ `=` $$\frac{40}{120}$$ Substitute the first and second term `=` `1/3` Simplify Next, substitute the known values to the formula`\text(First term)``[a]` `=` `120` `\text(Common Ratio)``[r]` `=` `1/3` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{120}}{1-\color{#00880A}{\frac{1}{3}}}$$ Substitute known values `=` `120/(2/3)` Evaluate `=` `180` `S_∞=180 \text(m)` -
Question 6 of 8
6. Question
A ball was dropped at a height of `10 \text(m)`. Find the limiting sum if the ball bounces back up by `\text(4/5)` of that height.
- `S_∞=` (90)` \text(m)`
Hint
Help VideoCorrect
Keep Going!
Incorrect
Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`First, find the value of the first term (`a`).The first term would be the first time the ball bounces, which is `\text(4/5)` of `10`.`10xx4/5` `=` `8` Substitute the known values to the formulaNote that the ball will be bouncing up and down each time, so the value must be multiplied by `2`.`r` `=` `4/5` `a` `=` `8` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ `=` $$2\left(\frac{\color{#e65021}{8}}{1-\color{#00880A}{\frac{4}{5}}}\right)$$ Substitute known values `=` $$2\left(\frac{8}{\frac{1}{5}}\right)$$ Evaluate `=` `2(40)` `=` `80` Finally, add the height from where the ball was first dropped, which is `10`.`S_∞` `=` `80` `+10` `=` `90` `S_∞=90 \text(m)` -
Question 7 of 8
7. Question
A speeding car brakes and travels `18` m in the first second, `4.5` m in the second, and `1.125` m in the third. How far will the car travel until it completely stops?
- `S_∞=` (24)` \text(m)`
Hint
Help VideoCorrect
Fantastic!
Incorrect
Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`Common Ratio Formula
$$\color{#00880A}{r}=\frac{U_2}{U_1}=\frac{U_3}{U_2}$$First, solve for the value of `r`.$$\color{#00880A}{r}$$ `=` $$\frac{U_2}{U_1}$$ `=` $$\frac{4.5}{18}$$ Substitute the first and second term `=` `1/4` Simplify Next, substitute the known values to the formula`\text(First term)``[a]` `=` `18` `\text(Common Ratio)``[r]` `=` `1/4` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{18}}{1-\color{#00880A}{\frac{1}{4}}}$$ Substitute known values `=` `18/(3/4)` Evaluate `=` `24` `S_∞=24 \text(m)` -
Question 8 of 8
8. Question
A man is standing on the roof of a building and drops a ball which travels `36`m onto the ground below. As it touches the ground, it goes back up `2/3` of its previous height and continues to dribble. Find out how high the ball rises after its sixth bounce.`(i)` How high would the ball rise after its sixth bounce?`(ii)` How many bounces will it take for the ball to have a height of `7 1/9`m?`(iii)` Find the total sum of the heights of the ball until it stopsRound off answer to `2` decimal places when applicable-
`(i)` (3.16)m`(ii)` (4) bounces`(iii)` (180)m
Hint
Help VideoCorrect
Excellent!
Incorrect
Common Ratio Formula
$$\color{#00880A}{r}=\frac{U_2}{U_1}=\frac{U_3}{U_2}$$Limiting Sum Formula
$$\color{#9a00c7}{S_∞}=\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$`\text(where) -1``<``r``<``1`General Rule of a Geometric Sequence
$$U_{\color{#9a00c7}{n}}=\color{#e65021}{a}\color{#00880A}{r}^{\color{#9a00c7}{n}-1}$$`(i)` Find how high the ball would rise after its sixth bounce.First, sketch the first few data on how the ball bounces.Note that each succeeding height is computed by getting `2/3` of the previous heightNext, substitute the known values to the general rule`\text(Number of terms)``[n]` `=` `6` `\text(First term)``[a]` `=` `24` `\text(Common Ratio)``[r]` `=` `2/3` $$U_{\color{#9a00c7}{n}}$$ `=` $$\color{#e65021}{a}\color{#00880A}{r}^{\color{#9a00c7}{n}-1}$$ $$U_{\color{#9a00c7}{6}}$$ `=` $$\color{#e65021}{24}\cdot\color{#00880A}{\frac{2}{3}}^{\color{#9a00c7}{6}-1}$$ Substitute known values `=` $$24\cdot\frac{2}{3}^5$$ Evaluate `=` $$24\cdot\frac{32}{243}$$ `=` `768/243` `=` `3.16`m The height of the ball after the sixth bounce is `3.16`m`(ii)` Find how many bounces it will take for the ball to have a height of `7 1/9`m.Substitute the known values to the general rule`\text(nth term)``[U_\color{#9a00c7}{n}]` `=` `7 1/9` `\text(First term)``[a]` `=` `24` `\text(Common Ratio)``[r]` `=` `2/3` $$U_{\color{#9a00c7}{n}}$$ `=` $$\color{#e65021}{a}\color{#00880A}{r}^{\color{#9a00c7}{n}-1}$$ $$7 \frac{1}{9}$$ `=` $$\color{#e65021}{24}\cdot\color{#00880A}{\frac{2}{3}}^{\color{#9a00c7}{n}-1}$$ Substitute known values `64/9``*1/24` `=` $$24\cdot\frac{2}{3}^{n-1}\color{#CC0000}{\cdot\frac{1}{24}}$$ Multiply both sides by `1/24` `8/27` `=` $$\frac{2}{3}^{n-1}$$ $$\log\frac{8}{27}$$ `=` $$\log{\frac{2}{3}^{n-1}}$$ Take the logarithm of both sides $$\log\frac{8}{27}$$ `=` $$(n-1)\log\frac{2}{3}$$ $$\frac{\log \frac{8}{27}}{\log \frac{2}{3}}$$ `=` $$n-1$$ $$1+\frac{\log \frac{8}{27}}{\log \frac{2}{3}}$$ `=` $$n$$ `1+3` `=` $$n$$ $$n$$ `=` `4` It takes `4` bounces for the ball to have a height of `7 1/9`m`(iii)` Find the total sum of the heights of the ball until it stops.First, substitute the known values to the limiting sum formula`\text(First term)``[a]` `=` `24` `\text(Common Ratio)``[r]` `=` `2/3` $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{a}}{1-\color{#00880A}{r}}$$ $$\color{#9a00c7}{S_∞}$$ `=` $$\frac{\color{#e65021}{24}}{1-\color{#00880A}{\frac{2}{3}}}$$ Substitute known values `=` `24/(1/3)` Evaluate `=` `72` This is just the total of the distances traveled by the ball from the air to the ground.It does not include the distance when it bounces from the ground back to the air and the initial height of `36`mFinally, double the limiting sum and add `36``2(72)+36` `=` `144+36` `=` `180`m The total sum of the heights of the ball until it stops is `180`m`(i) 3.16`m`(ii) 4` bounces`(iii) 180`m -




