Topics
>
Algebra 2>
Linear Equations and Graphs>
Slope Intercept Form: Graph an Equation>
Slope Intercept Form: Graph an Equation 2Slope Intercept Form: Graph an Equation 2
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 8 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- Answered
- Review
-
Question 1 of 8
1. Question
Graph y=34x-3y=34x−3
- 1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+by=mx+b
- mm is the gradient of the line
- bb is the y-intercept (where the line cuts the y-axis)
For: y=34x-3y=34x−3The gradient (m)(m) is 3434 and the y-intercept (b)(b) is -3−3.First, plot the y-intercept (-3)(−3)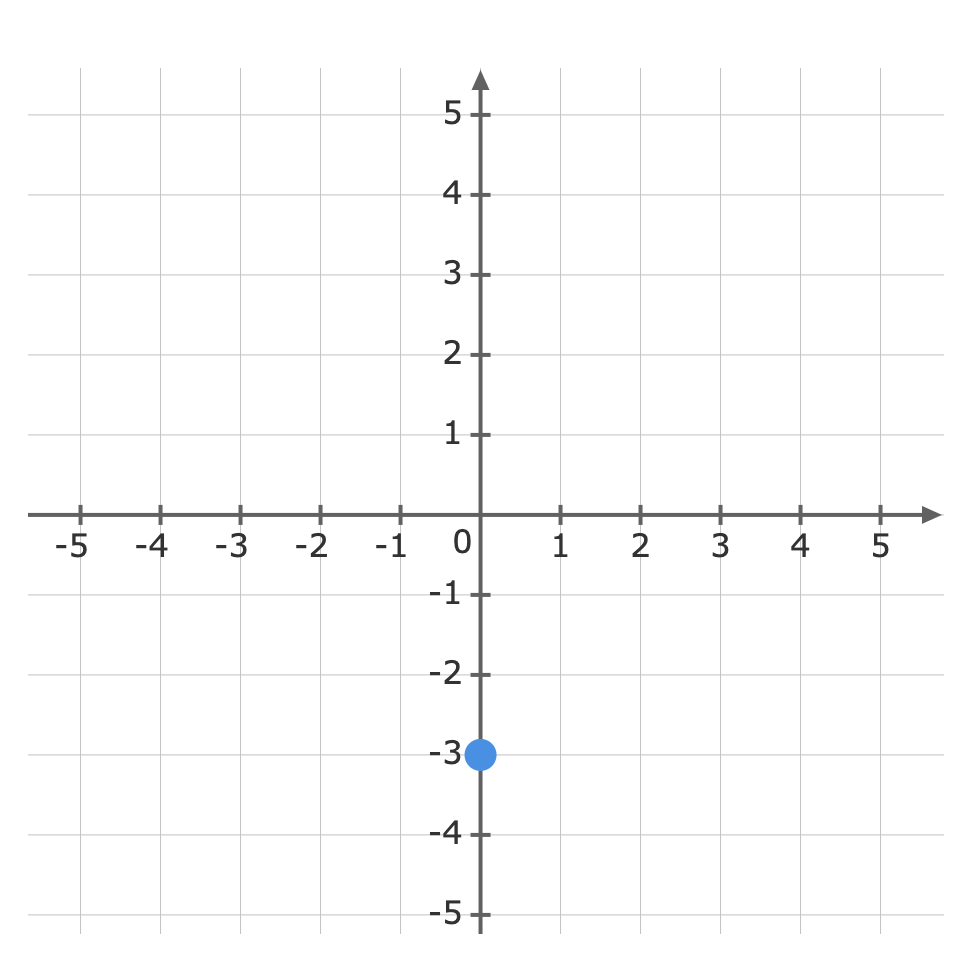 Use the gradient m=34m=34 to plot the next point.The gradient is equivalent to the rise over the run.riserun=34riserun=34From the y-intercept rise 33 units, then run 44 units to the right
Use the gradient m=34m=34 to plot the next point.The gradient is equivalent to the rise over the run.riserun=34riserun=34From the y-intercept rise 33 units, then run 44 units to the right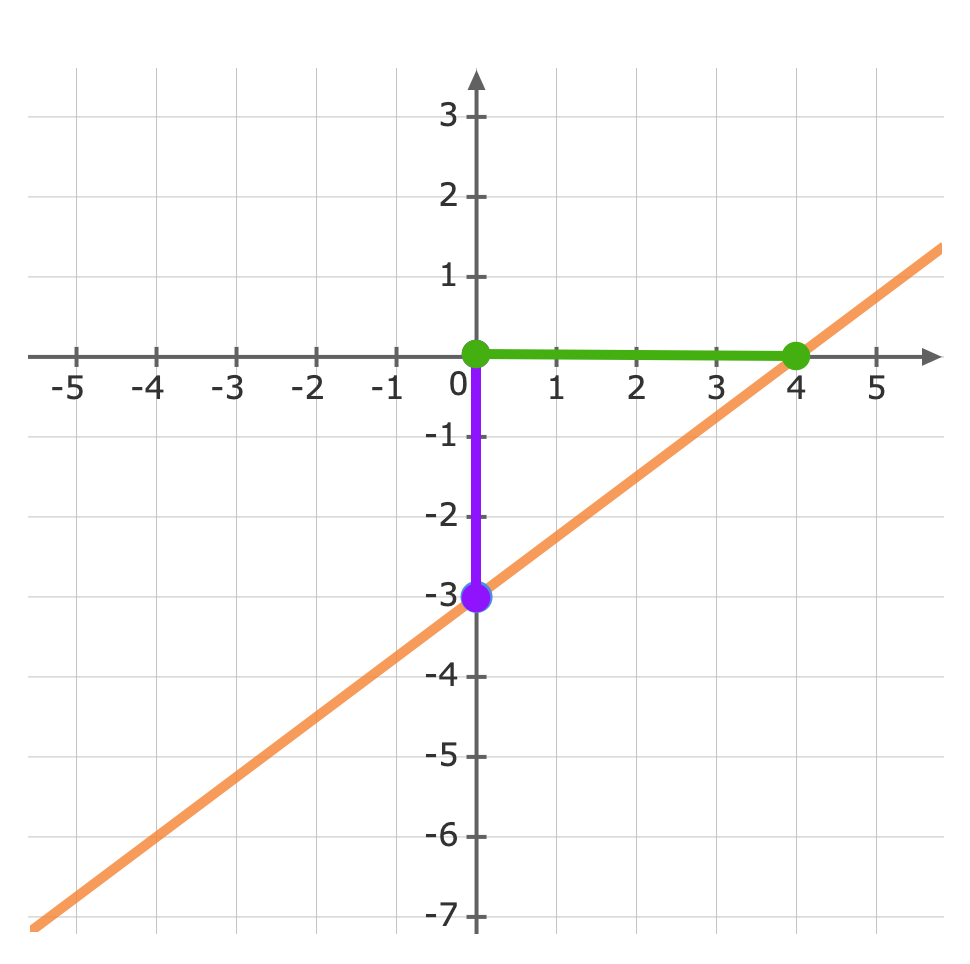 Now we can graph the equation
Now we can graph the equation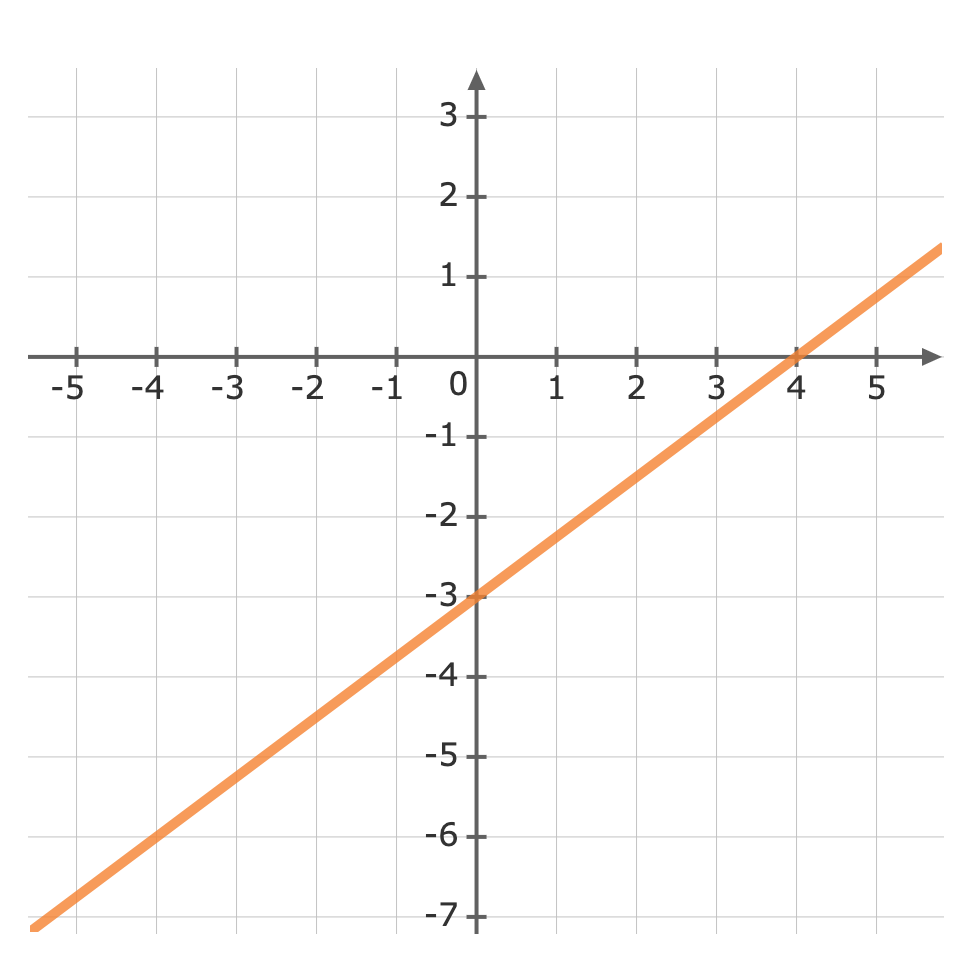
-
Question 2 of 8
2. Question
Graph y=-14x+3y=−14x+3
-
1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+by=mx+b
- mm is the gradient of the line
- bb is the y-intercept (where the line cuts the y-axis)
For: y=-14x+3y=−14x+3The gradient (m)(m) is -14−14 and the y-intercept (b)(b) is 33.First, plot the y-intercept (3)(3)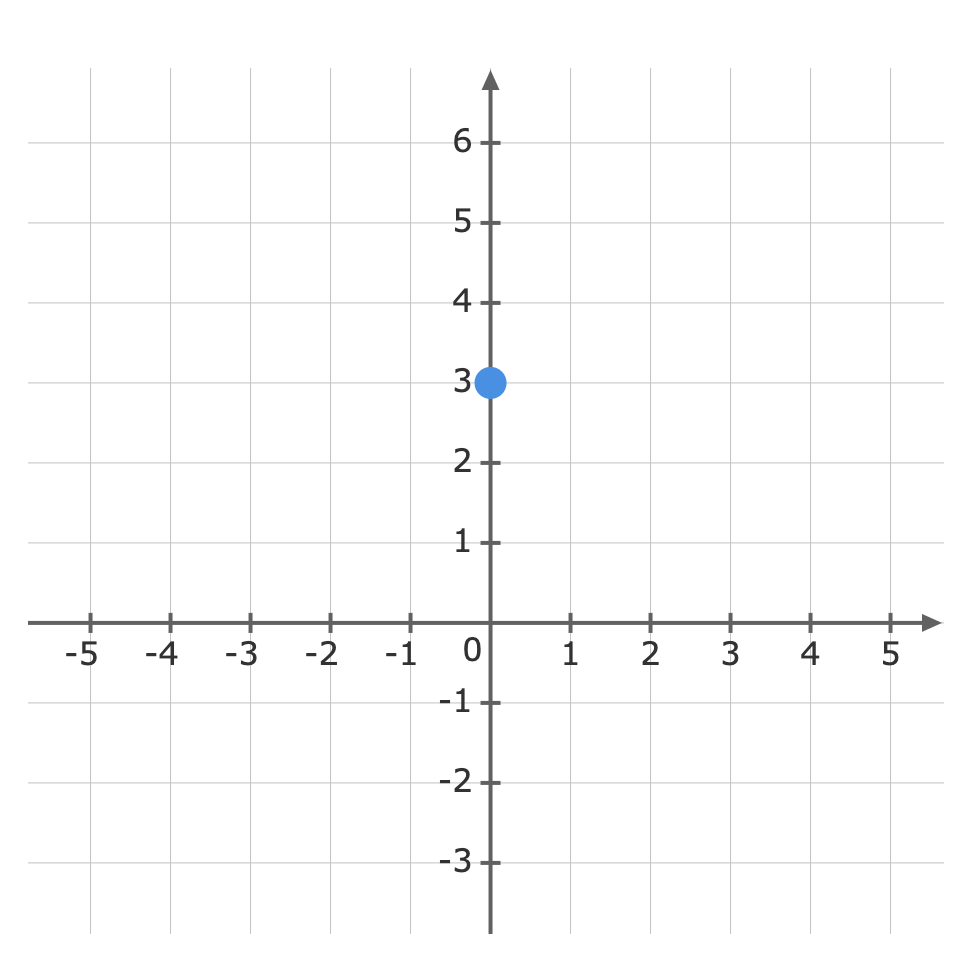 Use the gradient m=-14m=−14 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-14riserun=−14From the y-intercept rise -1−1 units, then run 44 units to the right
Use the gradient m=-14m=−14 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-14riserun=−14From the y-intercept rise -1−1 units, then run 44 units to the right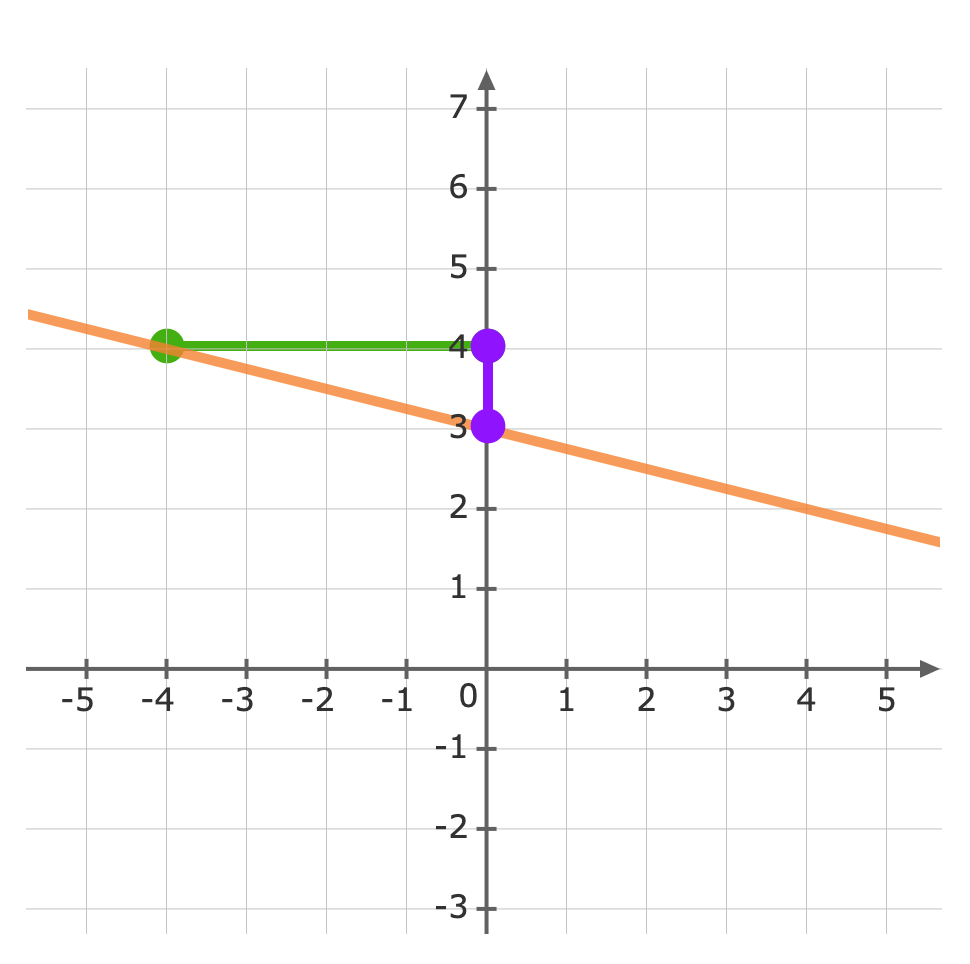 Now we can graph the equation
Now we can graph the equation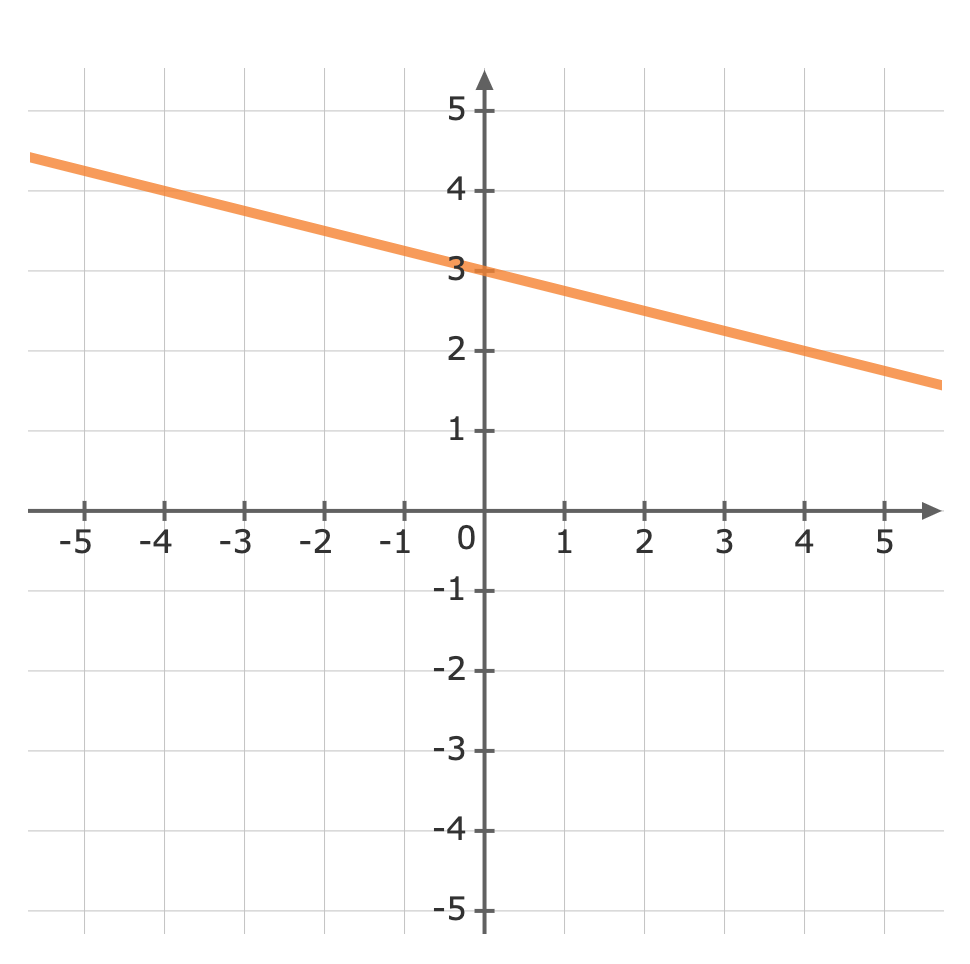
-
1.
-
Question 3 of 8
3. Question
Graph y=53x+1y=53x+1
-
1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+by=mx+b
- m is the gradient of the line
- b is the y-intercept (where the line cuts the y-axis)
For: y=53x+1The gradient (m) is 53 and the y-intercept (b) is 1.First, plot the y-intercept (1)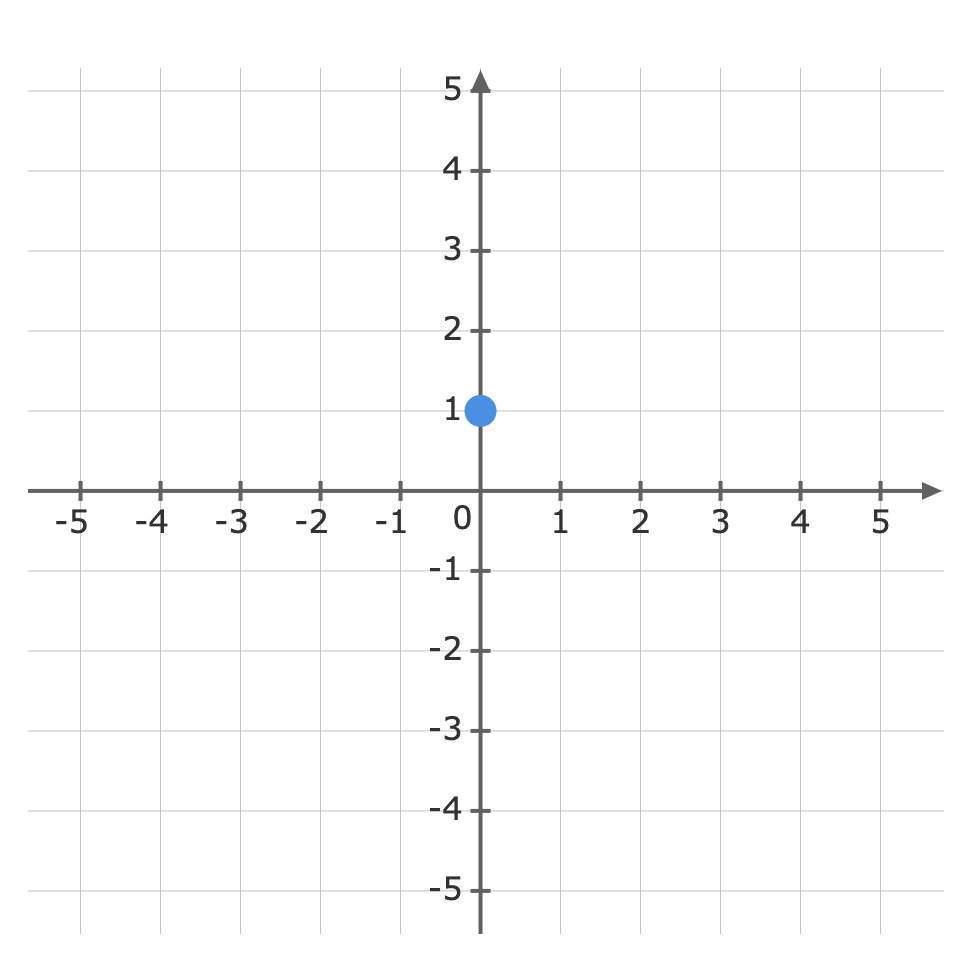 Use the gradient m=53 to plot the next point.The gradient is equivalent to the rise over the run.riserun=53From the y-intercept rise 5 units, then run 3 units to the right
Use the gradient m=53 to plot the next point.The gradient is equivalent to the rise over the run.riserun=53From the y-intercept rise 5 units, then run 3 units to the right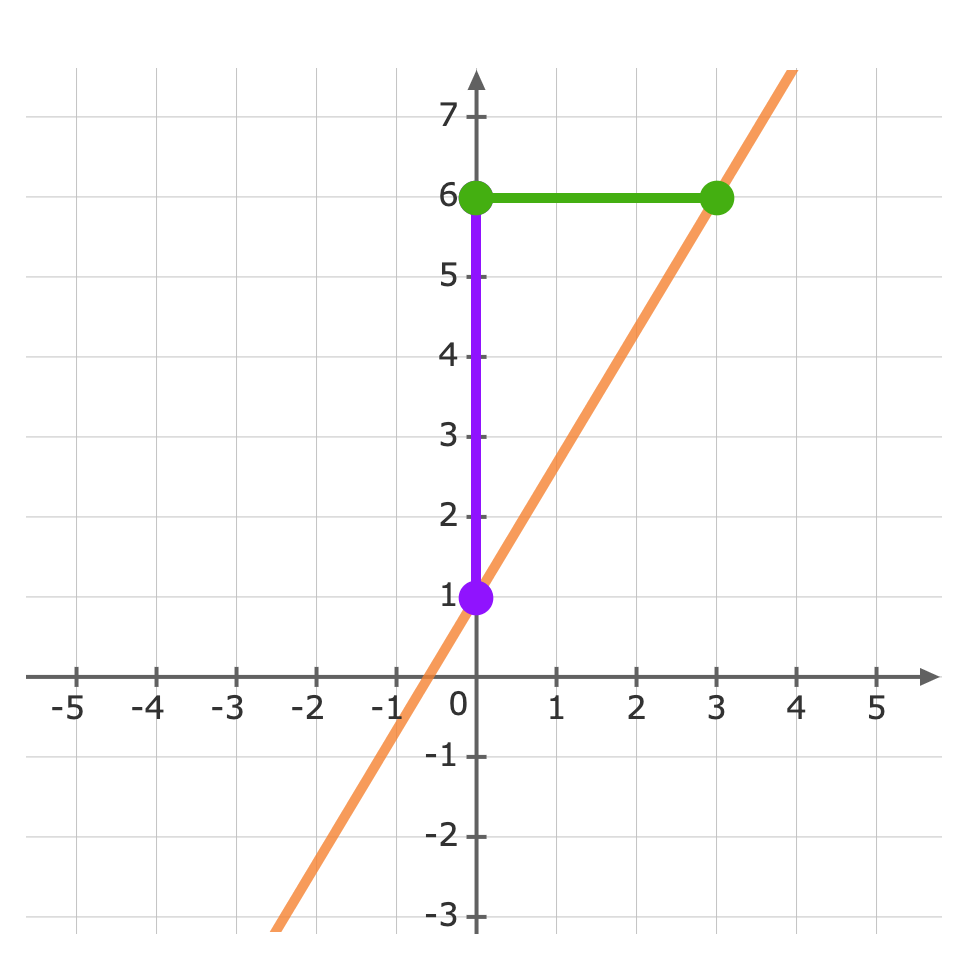 Now we can graph the equation
Now we can graph the equation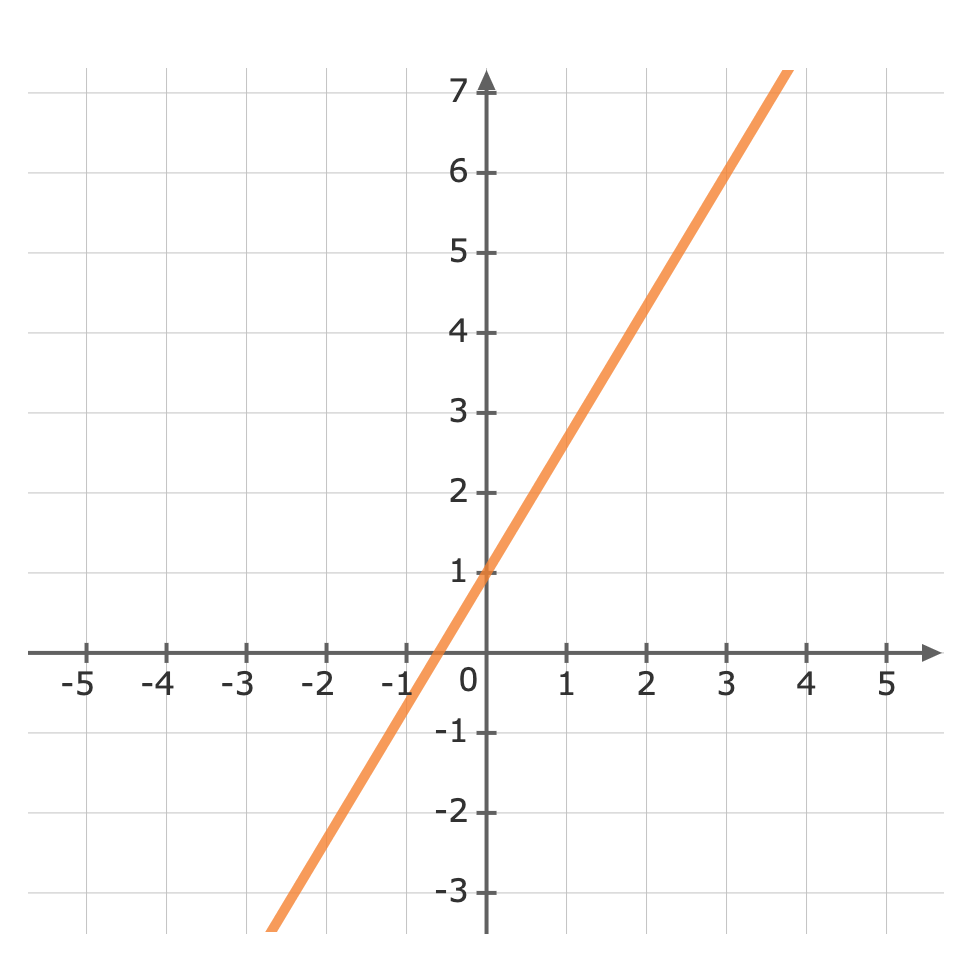
-
1.
-
Question 4 of 8
4. Question
Graph y=-58x+2
-
1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+b
- m is the gradient of the line
- b is the y-intercept (where the line cuts the y-axis)
For: y=-58x+2The gradient (m) is -58 and the y-intercept (b) is 2.First, plot the y-intercept (2)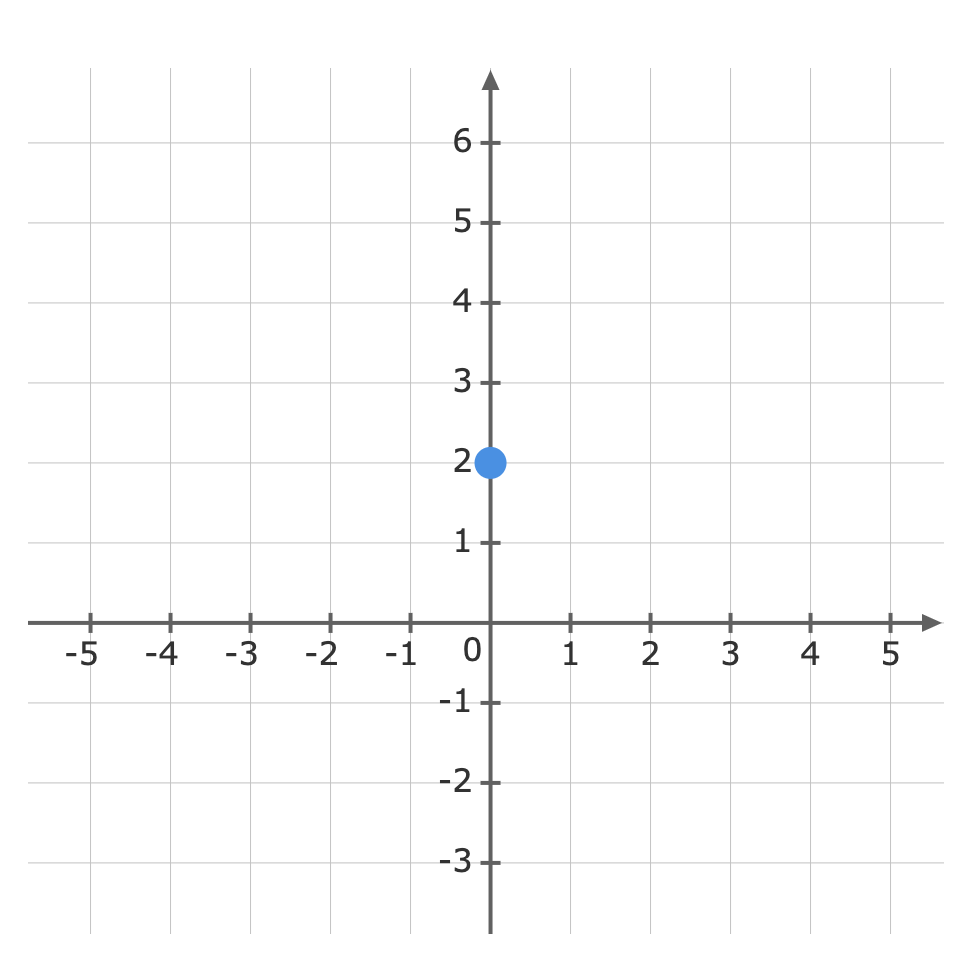 Use the gradient m=-58 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-58From the y-intercept move down -5 units, then run 8 units to the right
Use the gradient m=-58 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-58From the y-intercept move down -5 units, then run 8 units to the right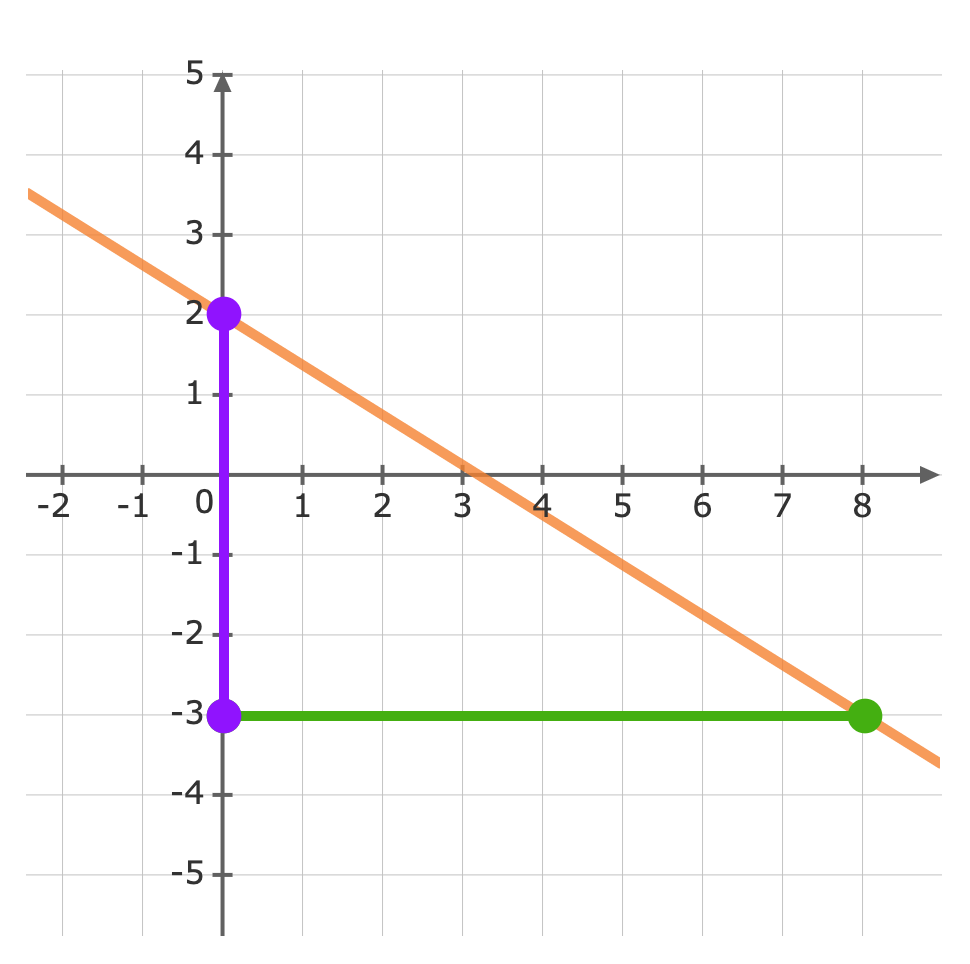 Now we can graph the equation
Now we can graph the equation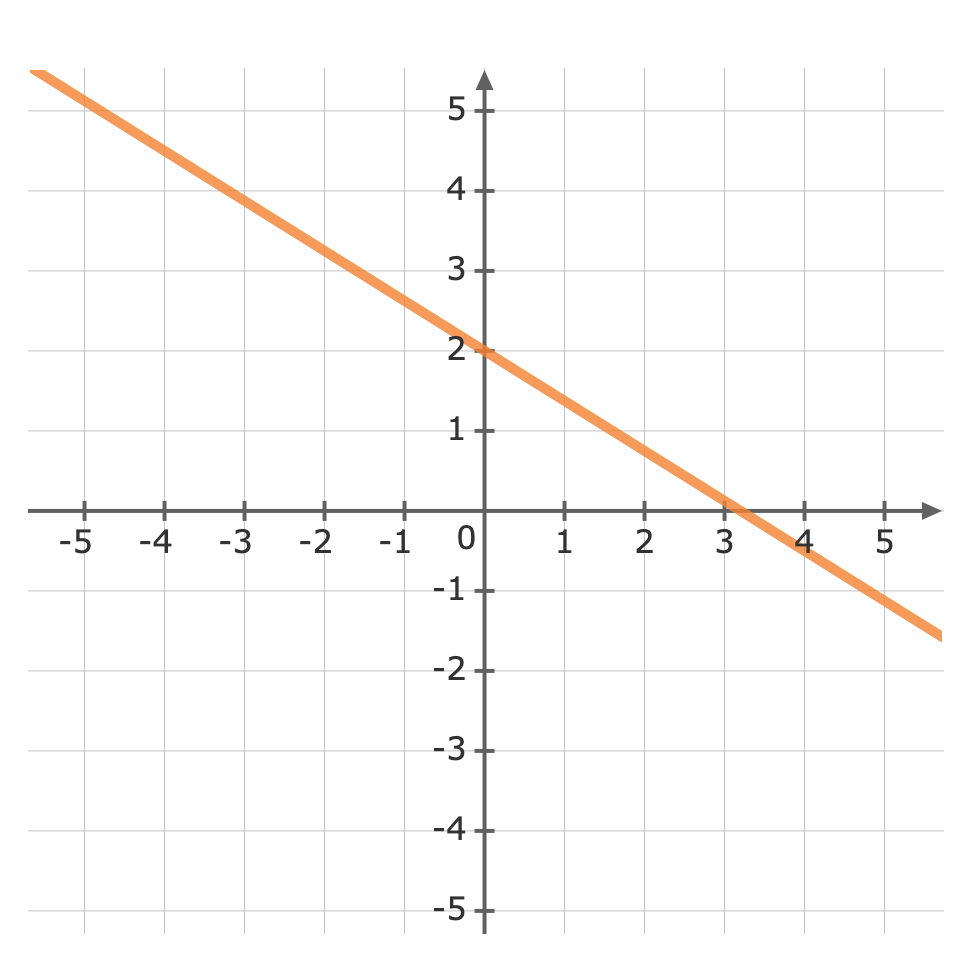
-
1.
-
Question 5 of 8
5. Question
Graph y=-3x+3
-
1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+b
- m is the gradient of the line
- b is the y-intercept (where the line cuts the y-axis)
For: y=-3x+3The gradient (m) is -3 and the y-intercept (b) is 3.First, plot the y-intercept (3) Use the gradient m=-3 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-31From the y-intercept move down -3 units, then run 1 unit to the right
Use the gradient m=-3 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-31From the y-intercept move down -3 units, then run 1 unit to the right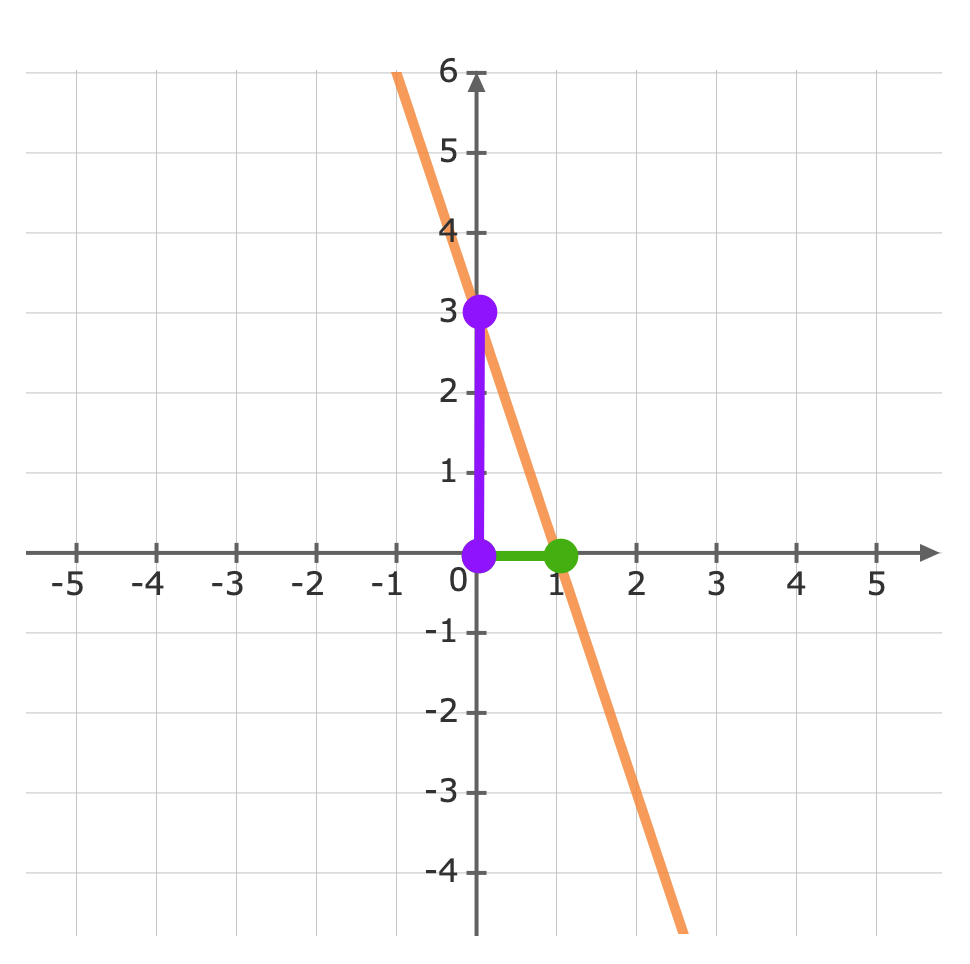 Now we can graph the equation
Now we can graph the equation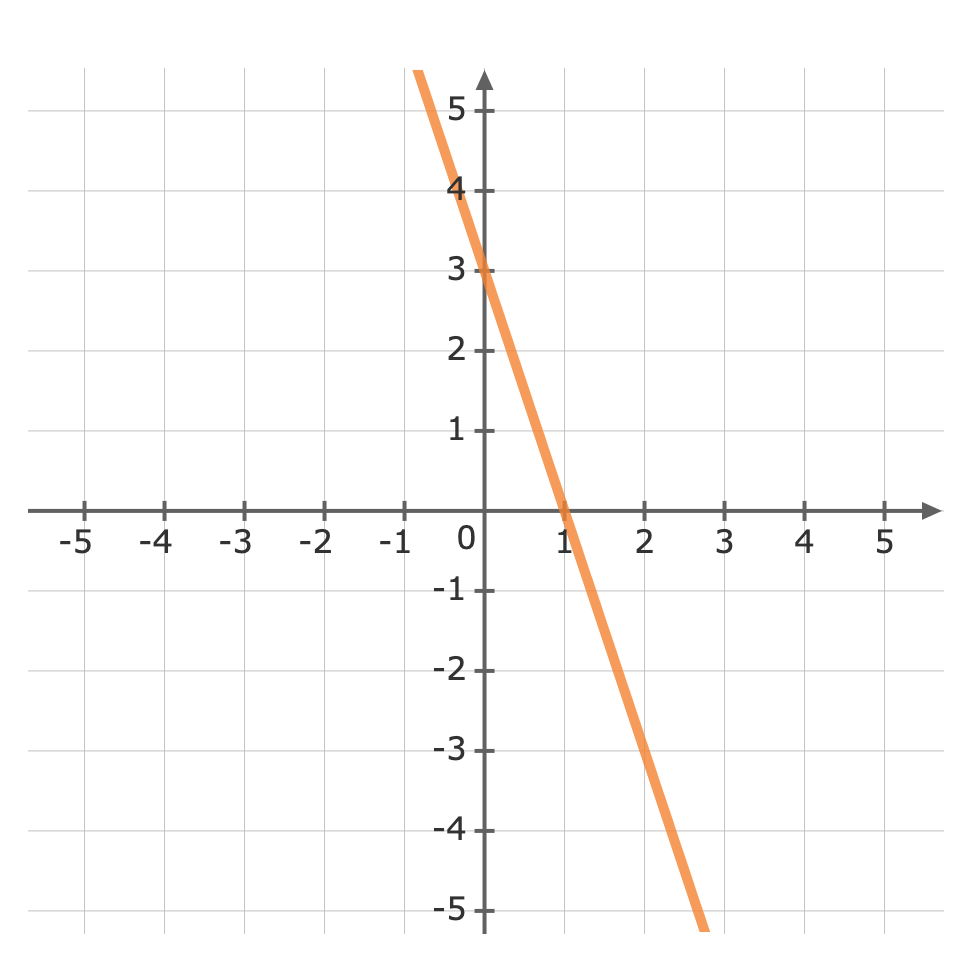
-
1.
-
Question 6 of 8
6. Question
Graph y=2x-5
-
1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+b
- m is the gradient of the line
- b is the y-intercept (where the line cuts the y-axis)
For: y=2x-5The gradient (m) is 2 and the y-intercept (b) is -5.First, plot the y-intercept (-5)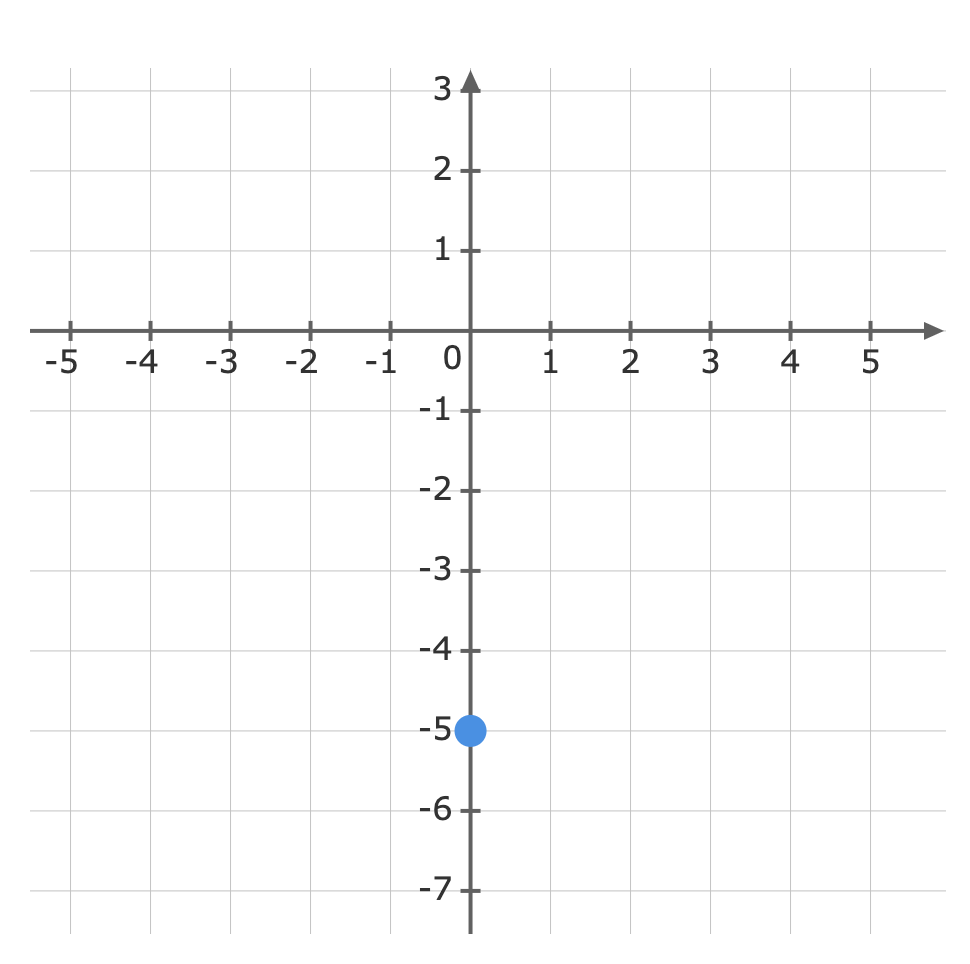 Use the gradient m=2 to plot the next point.The gradient is equivalent to the rise over the run.riserun=21From the y-intercept rise 2 units, then run 1 units to the right
Use the gradient m=2 to plot the next point.The gradient is equivalent to the rise over the run.riserun=21From the y-intercept rise 2 units, then run 1 units to the right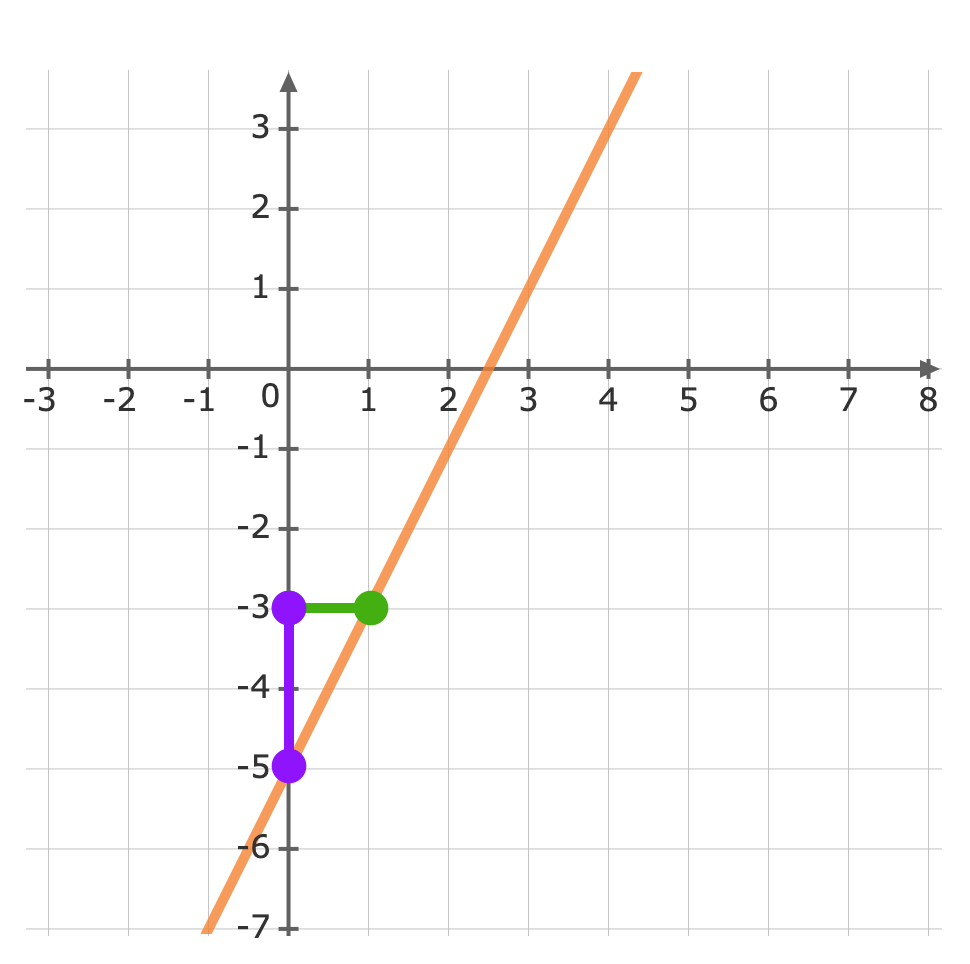 Now we can graph the equation
Now we can graph the equation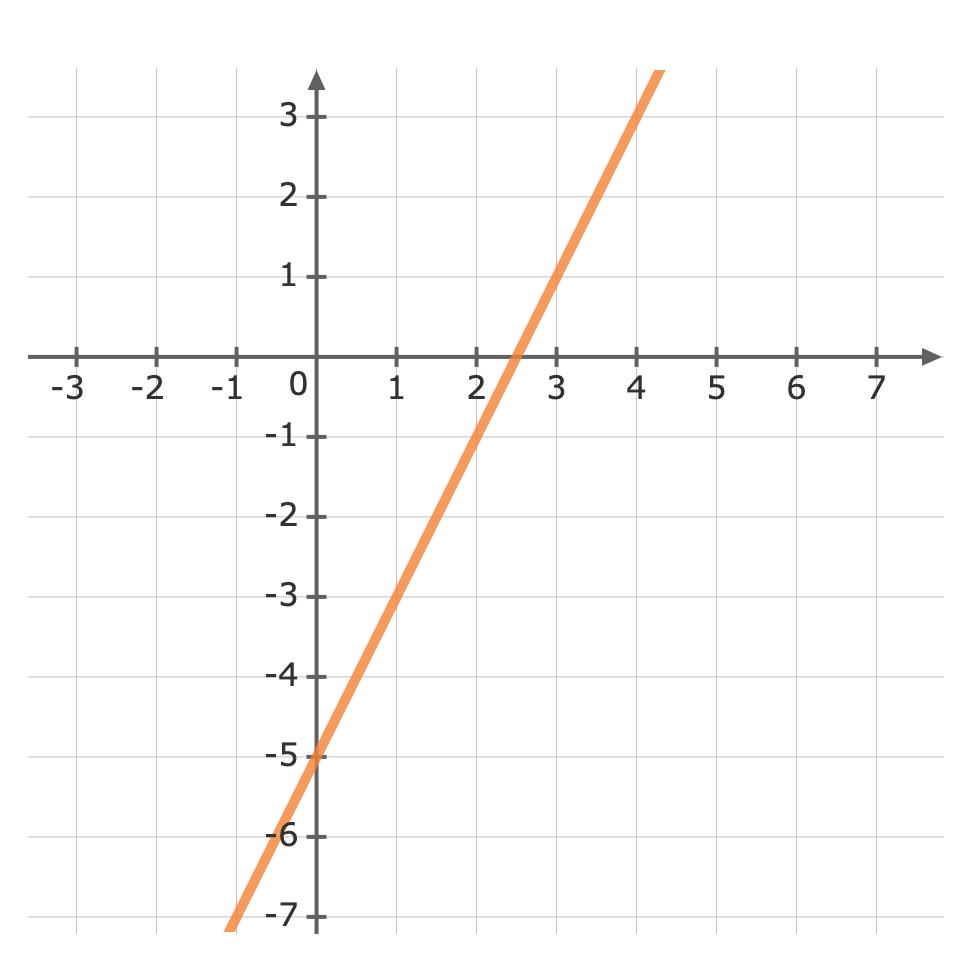
-
1.
-
Question 7 of 8
7. Question
Graph y=45x+3
-
1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+b
- m is the gradient of the line
- b is the y-intercept (where the line cuts the y-axis)
For: y=45x+3The gradient (m) is 45 and the y-intercept (b) is 3.First, plot the y-intercept (3) Use the gradient m=45 to plot the next point.The gradient is equivalent to the rise over the run.riserun=45From the y-intercept rise 4 units, then run 5 units to the right
Use the gradient m=45 to plot the next point.The gradient is equivalent to the rise over the run.riserun=45From the y-intercept rise 4 units, then run 5 units to the right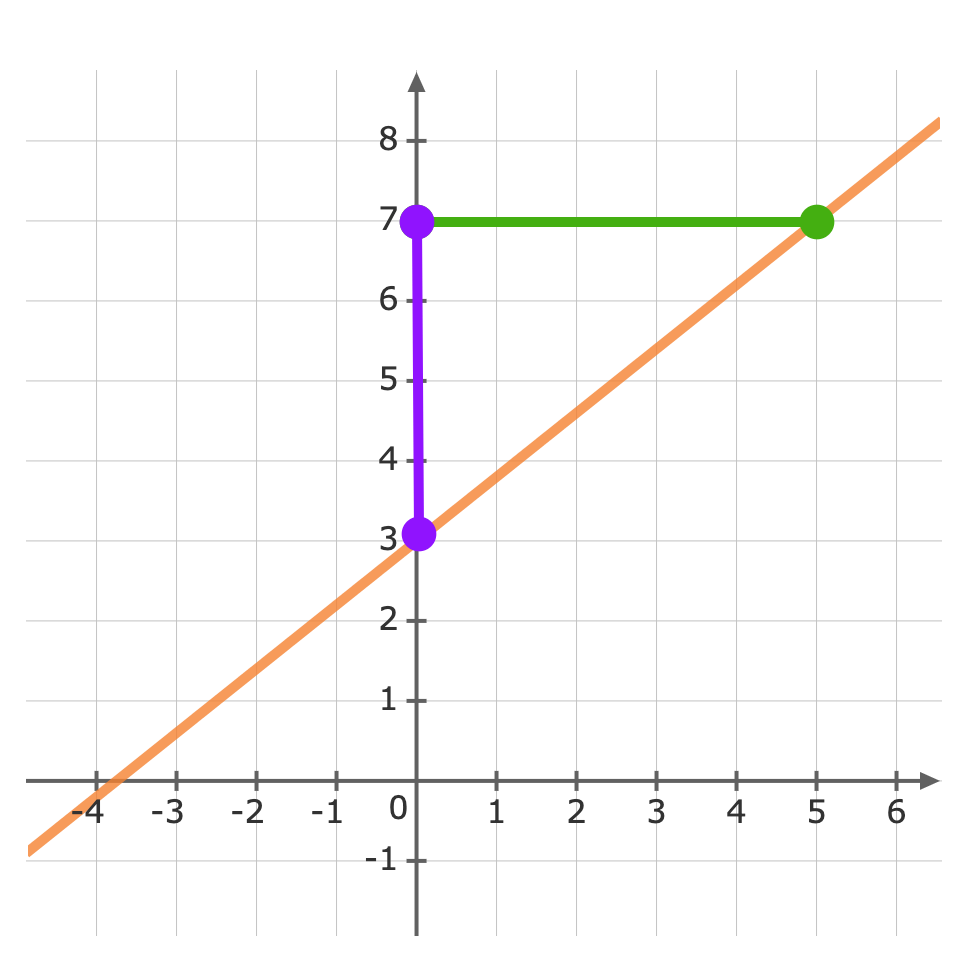 Now we can graph the equation
Now we can graph the equation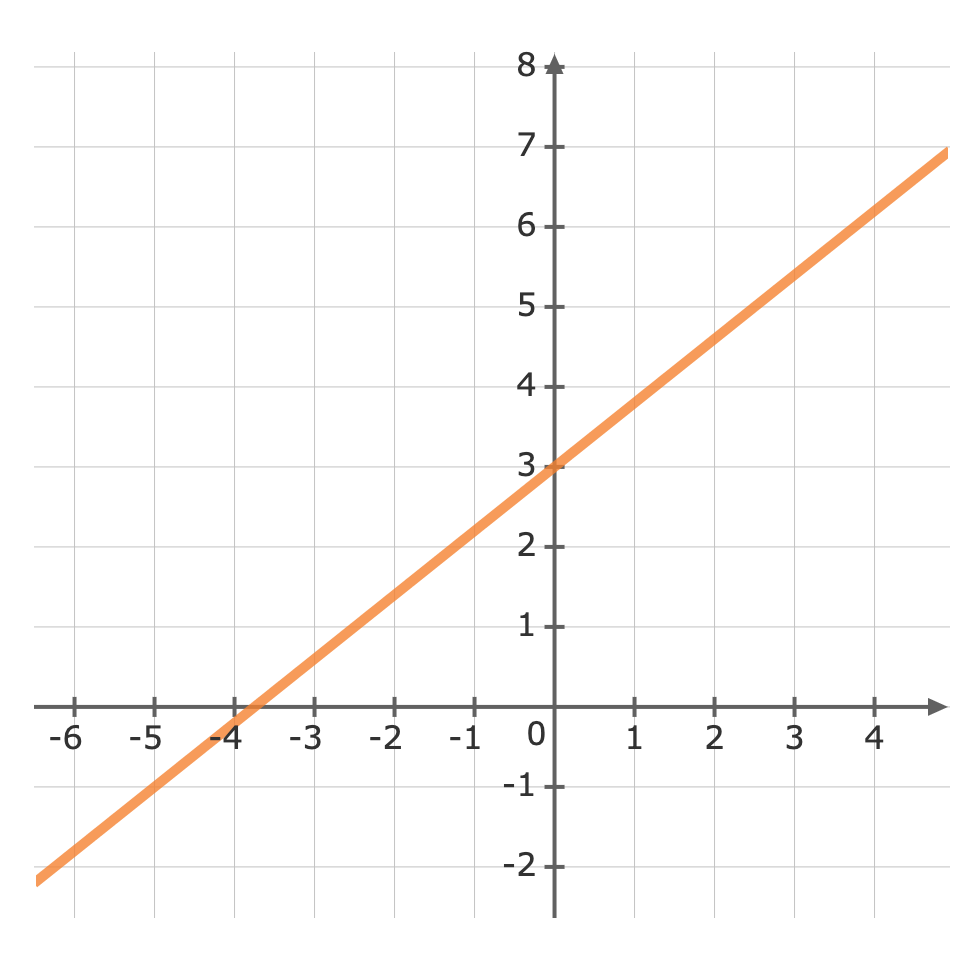
-
1.
-
Question 8 of 8
8. Question
Graph y=-38x-4
-
1.
-
2.
-
3.
-
4.
Correct
Keep Going!
Incorrect
Gradient Intercept Form: y=mx+b
- m is the gradient of the line
- b is the y-intercept (where the line cuts the y-axis)
For: y=-38x-4The gradient (m) is -38 and the y-intercept (b) is -4.First, plot the y-intercept (-4)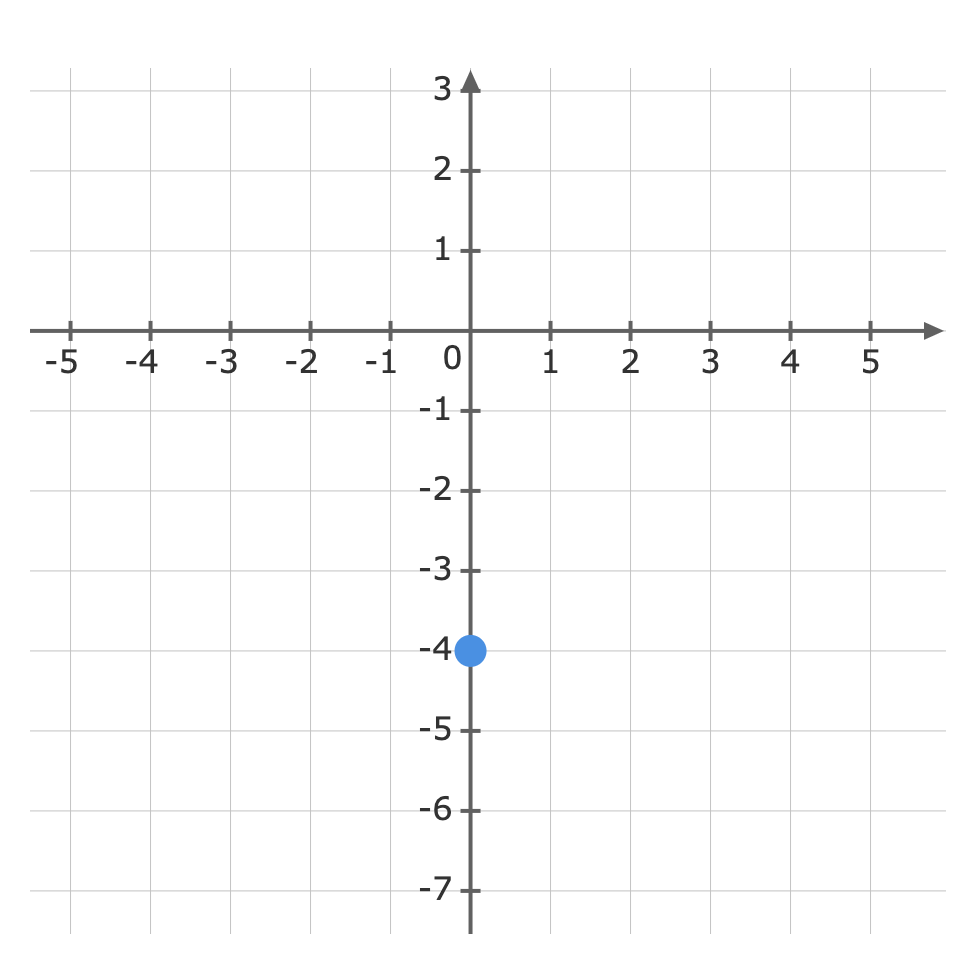 Use the gradient m=-38 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-38From the y-intercept rise -3 units, then run 8 units to the right
Use the gradient m=-38 to plot the next point.The gradient is equivalent to the rise over the run.riserun=-38From the y-intercept rise -3 units, then run 8 units to the right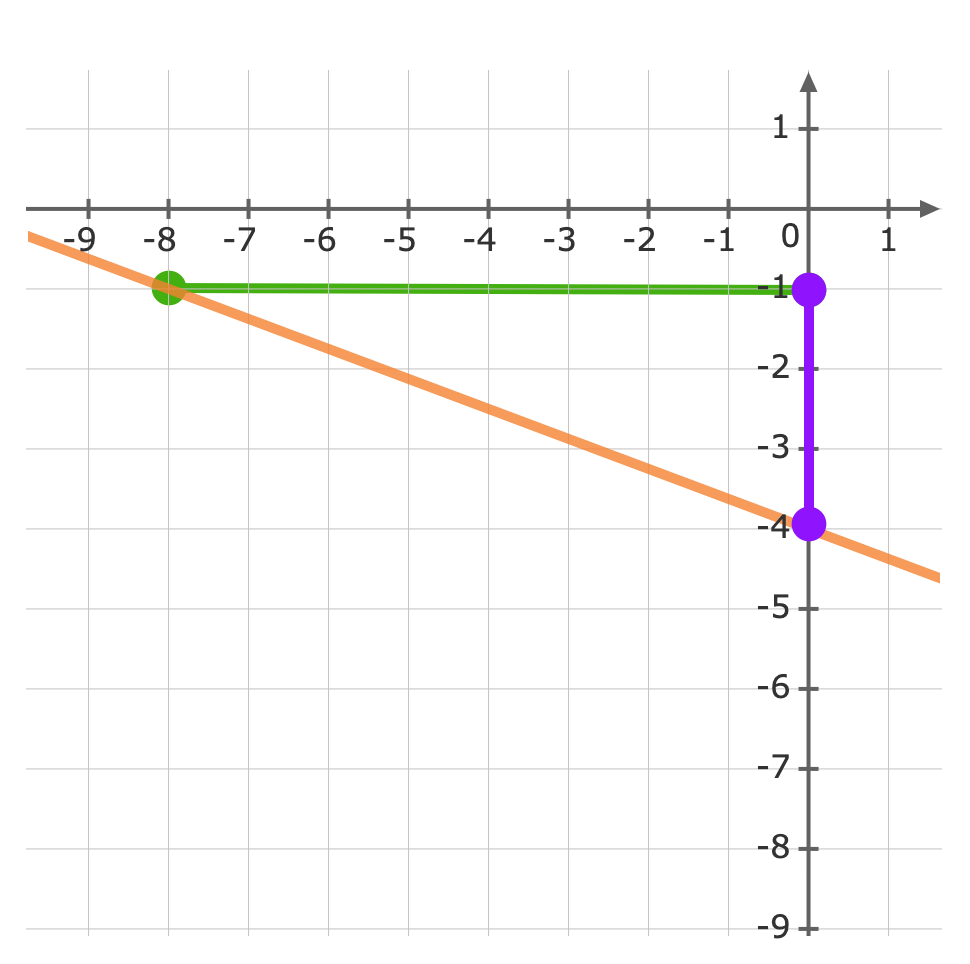 Now we can graph the equation
Now we can graph the equation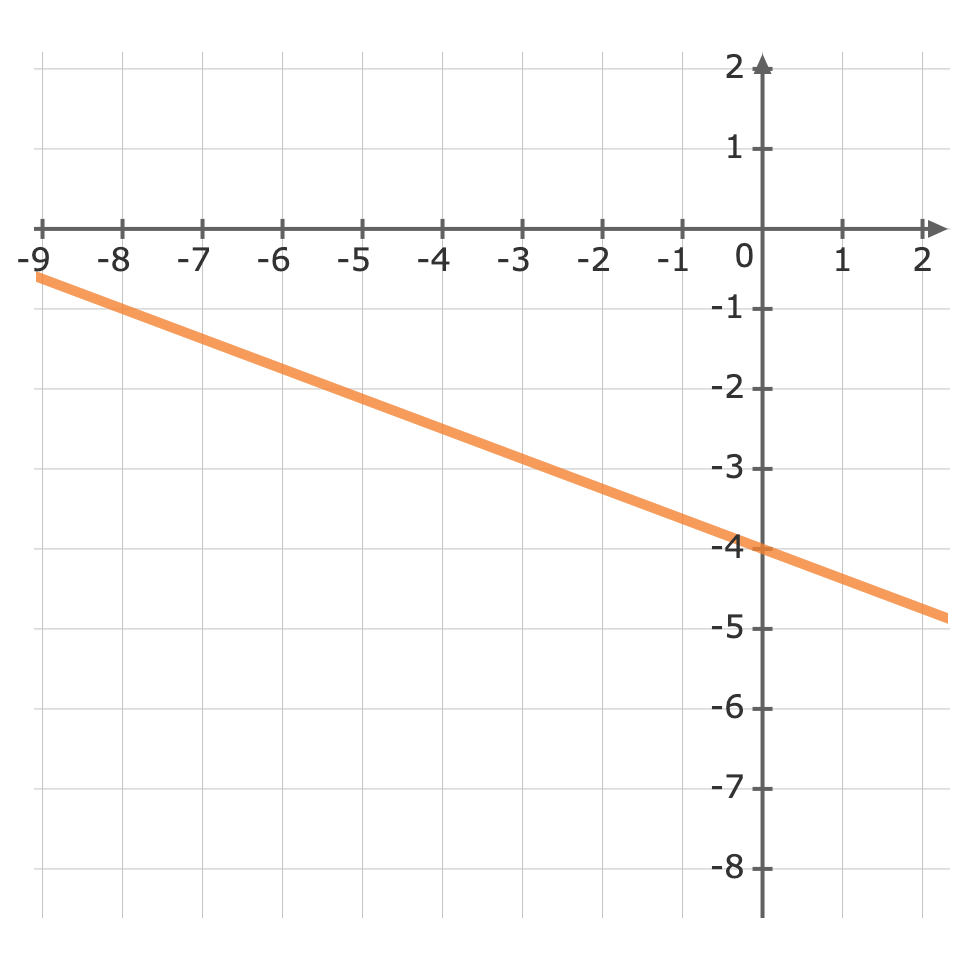
-
1.
Quizzes
- Distance Between Two Points 1
- Distance Between Two Points 2
- Distance Between Two Points 3
- Midpoint of a Line 1
- Midpoint of a Line 2
- Midpoint of a Line 3
- Slope of a Line 1
- Slope of a Line 2
- Slope Intercept Form: Graph an Equation 1
- Slope Intercept Form: Graph an Equation 2
- Slope Intercept Form: Write an Equation 1
- Graph Linear Inequalities 1
- Convert Standard Form and Slope Intercept Form 1
- Convert Standard Form and Slope Intercept Form 2
- Point Slope Form 1
- Point Slope Form 2
- Parallel Lines 1
- Parallel Lines 2
- Perpendicular Lines 1
- Perpendicular Lines 2






























