Topics
>
Algebra 2>
Conic Sections>
Write an Equation for Cubic Curves>
Write an Equation for Cubic CurvesWrite an Equation for Cubic Curves
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 7 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
- 6
- 7
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- Answered
- Review
-
Question 1 of 7
1. Question
Write the equation of the cubic graph that is shown on the number plane below.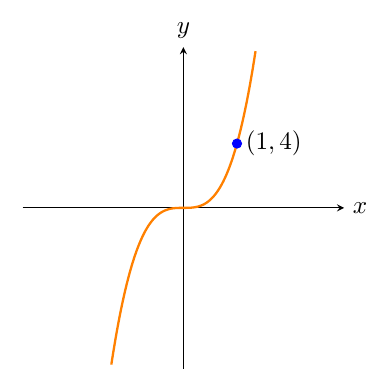
Hint
Help VideoCorrect
Great Work!
Incorrect
This cubic curve does not have any turning points and it passes through the origin. Therefore it is in the form `y=ax^3`.Use the point `(1,4)` shown on the graph to find the value of `a`.The `x`-coordinate of this point is `1`, and the `y`-coordinate of this point is `4`.So we should substitute `x=1` and `y=4` into the equation `y``=a``x^3`.`4``=a(``1^3``)`.Solve this equation to find the value of `a`.`a=4`Substitute the value for `a` and write the equation of the graph.`y=4x^3` -
Question 2 of 7
2. Question
Write the equation of the cubic graph that is shown on the number plane below.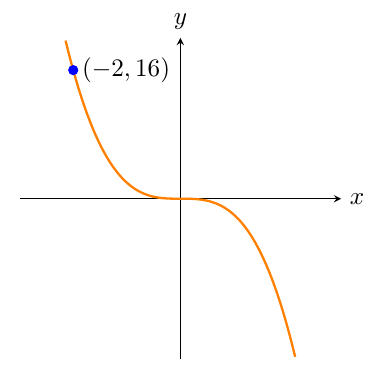
Hint
Help VideoCorrect
Correct!
Incorrect
This cubic curve does not have any turning points and it passes through the origin. Therefore it is in the form `y=ax^3`.Use the point `(-2,16)` shown on the graph to find the value of `a`.The `x`-coordinate of this point is `-2`, and the `y`-coordinate of this point is `16`.So we should substitute `x=-2` and `y=16` into the equation `y``=a``x^3`.`16``=a``(-2)^3`.Solve this equation to find the value of `a`.`16=-8a``\frac{16}{-8}=a``a=-2`Substitute the value for `a` and write the equation of the graph.`y=-2x^3` -
Question 3 of 7
3. Question
Write the equation of the cubic graph that is shown on the number plane below.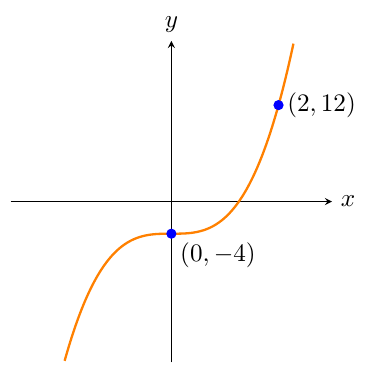
Hint
Help VideoCorrect
Keep Going!
Incorrect
This cubic curve does not have any turning points and it passes through the origin. Therefore it is in the form `y=ax^3`.The value of `d` will be given by the `y`-intercept.The graph crosses the `y`-axis at `(0,``-4``)`, therefore `d=-4`.The equation of the graph has the form `y=ax^3 ``-4`.Use the point `(2,12)` shown on the graph to find the value of `a`.The `x`-coordinate of this point is `2`, and the `y`-coordinate of this point is `12`.So we should substitute `x=2` and `y=12` into the equation `y``=a``x^3``-4`.`12``=a``(2^3)``-4`.Solve this equation to find the value of `a`.`12=8a-4``16=8a``\frac{16}{8}=a``a=2`Substitute the value for `a` and write the equation of the graph.`y=2x^3-4` -
Question 4 of 7
4. Question
Write the equation of the cubic graph that is shown on the number plane below.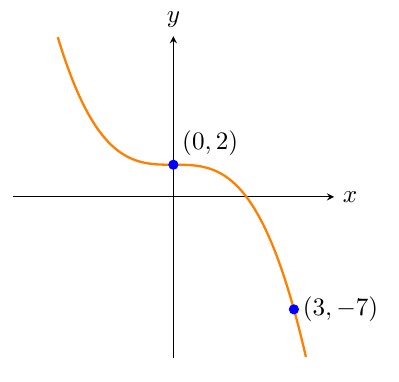
Hint
Help VideoCorrect
Fantastic!
Incorrect
This cubic curve does not have any turning points and it passes through the origin. Therefore it is in the form `y=ax^3`.The value of `d` will be given by the `y`-intercept.The graph crosses the `y`-axis at `(0,``2``)`, therefore `d=2`.The equation of the graph has the form `y=ax^3 ``+2`.Use the point `(3,-7)` shown on the graph to find the value of `a`.The `x`-coordinate of this point is `3`, and the `y`-coordinate of this point is `-7`.So we should substitute `x=3` and `y=-7` into the equation `y``=a``x^3``+2`.`-7``=a``(3^3)``+2`.Solve this equation to find the value of `a`.`-7=27a+2``-9=27a``-\frac{27}{9}=a``a=-\frac{1}{3}`Substitute the value for `a` and write the equation of the graph.`y=-\frac{1}{3}x^3+2` -
Question 5 of 7
5. Question
Write the equation of the cubic graph that is shown on the number plane below.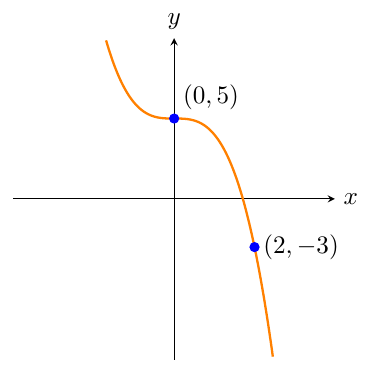
Hint
Help VideoCorrect
Excellent!
Incorrect
This cubic curve does not have any turning points and it passes through the origin. Therefore it is in the form `y=ax^3`.The value of `d` will be given by the `y`-intercept.The graph crosses the `y`-axis at `(0,``5``)`, therefore `d=5`.The equation of the graph has the form `y=ax^3 ``+5`.Use the point `(2,-3)` shown on the graph to find the value of `a`.The `x`-coordinate of this point is `2`, and the `y`-coordinate of this point is `-3`.So we should substitute `x=2` and `y=-3` into the equation `y``=a``x^3``+5`.`-3``=a``(2^3)``+5`.Solve this equation to find the value of `a`.`-3=8a+5``-8=8a``\frac{-8}{8}=a``a=-1`Substitute the value for `a` and write the equation of the graph.`y=-x^3+5` -
Question 6 of 7
6. Question
The following equation is graphed below:
`y=a(x-1)(x+1)(x-3)`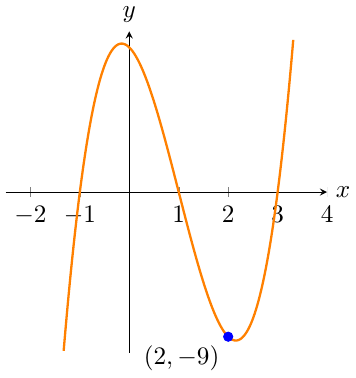
What is the value of `a`?Hint
Help VideoCorrect
Fantastic!
Incorrect
The standard form for graphing a cubic is `y=a(x-r)(x-s)(x-t)`.Since the point `(``2``,``-9``)` lies on the graph we can substitute `x=2` and `y=-9` into the equation and solve to find `a`.`-9``=a(``2``-1)(``2``+1)(``2``-3)``-9=a(1)(3)(-1)``-9=-3a``\frac{-9}{-3}=a``a=3` -
Question 7 of 7
7. Question
Write the equation of the cubic graph shown below.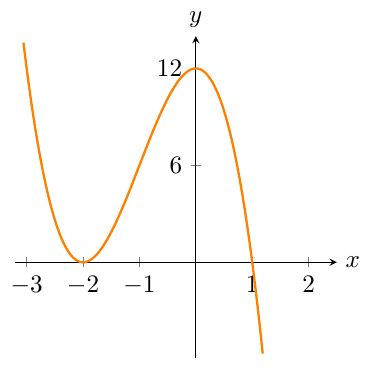
Hint
Help VideoCorrect
Exceptional!
Incorrect
The standard form for graphing a cubic is `y=a(x-r)(x-s)(x-t)`, where `r`, `s`, and `t` are the `x`-intercepts of the graph.Find the values of the `x`-intercepts of the graph.One `x`-intercept is at `1`, so `r=1`.The graph touches the `x`-axis at `-2`, meaning it will be a repeated root, so `s=-2` and `t=-2`Substitute the values for `r`, `s` and `t` into the standard equation`y=a(x-``1``)(x-(``-2``))(x-(``-2``))``y=a(x-1)(x+2)^2`Since the graph passes through `(``0``,``12``)`, substitute `x=0` and `y=12` into the equation and solve to find `a`.`12``=a(``0``-1)(``0``+2)^2``12=a(-1)(2)^2``12=-4a``\frac{12}{-4}=a``a=-3`Substitute the value for `a` and write the complete equation.`y=-3(x-1)(x+2)^2`
Quizzes
- Write an Equation for Circle Graphs
- Graph Circles in Standard Form
- Graph Circles in Expanded Form
- Graph Parabolas (Focus and Directrix) 1
- Graph Parabolas (Focus and Directrix) 2
- Graph Parabolas Given the Vertex, Focus and Directrix 1
- Graph Parabolas Given the Vertex, Focus and Directrix 2
- Graph Hyperbolas
- Write an Equation for Hyperbolas
- Graph Cubic Curves
- Write an Equation for Cubic Curves
- The Exponential Curve