Shortest Path 1
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 4 questions completed
Questions:
- 1
- 2
- 3
- 4
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- Answered
- Review
-
Question 1 of 4
1. Question
Find the shortest path from `A` to all other points.
-
`\text(From)` `A` `\text(To)` `B` (7) `C` (13) `D` (15) `E` (8) `F` (1) `G` (5) `H` (9)
Hint
Help VideoCorrect
Great Work!
Incorrect
Dijkstra’s Algorithm is a method of finding a shortest path from a vertex to another by comparing multiple paths and finding the shortest value or sum of values.First, mark the starting vertex, which is `A`.
Next, start finding the shortest paths to the closest vertices, which are `B`, `G`, and `F`.Always check for multiple paths and find the one with the lowest value.`F` `:` `1` 
`G` `:` `5` 
`B` `:` `8` or `7` 
Now start finding the shortest paths to the remaining vertices, which are `E`, `H`, `C` and `D`.Always check for multiple paths and find the one with the lowest value.`E` `:` `11` or `8` 
`H` `:` `13, 10` or `9` 
`C` `:` `16` or `13` 
`D` `:` `21` or `15` 
Finally, fill in the table with the values of the shortest paths.`\text(From)` `A` `\text(To)` `B` `7` `C` `13` `D` `15` `E` `8` `F` `1` `G` `5` `H` `9` -
-
Question 2 of 4
2. Question
The diagram shows the biking track around a park reserve. The values are the kilometres to be traveled to reach each point. Find the shortest path from point `P` to all the other points.
-
`\text(From)` `P` `\text(To)` `Q` (3) `R` (5) `S` (7) `T` (8) `U` (6) `V` (2) `W` (1) `X` (4) `Y` (6)
Hint
Help VideoCorrect
Correct!
Incorrect
Dijkstra’s Algorithm is a method of finding a shortest path from a vertex to another by comparing multiple paths and finding the shortest value or sum of values.First, mark the starting vertex, which is `P`.
Next, start finding the shortest paths to the closest vertices, which are `Q`, `W`, and `V`.Always check for multiple paths and find the one with the lowest value.`Q` `:` `4` or `3` 
`W` `:` `1`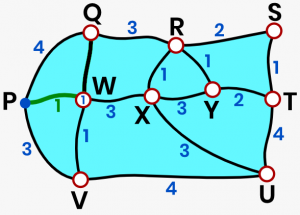 
`V` `:` `3` or `2`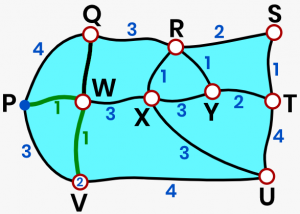 
Now start finding the shortest paths to the vertices two edges away from `P`, which are `R`, and `X`.Always check for multiple paths and find the one with the lowest value.`R` `:` `6` or `5`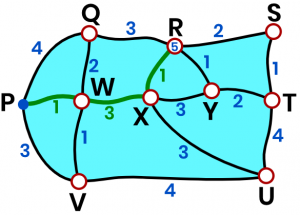 
`X` `:` `4`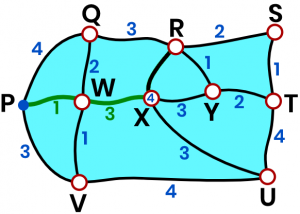 
Now start finding the shortest paths to the remaining vertices, which are `Y`, `S`, `T`, and `U`.Always check for multiple paths and find the one with the lowest value.`Y` `:` `7` or `6`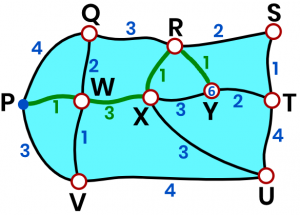 
`S` `:` `7`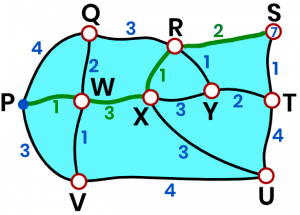 
`T` `:` `10` or `8`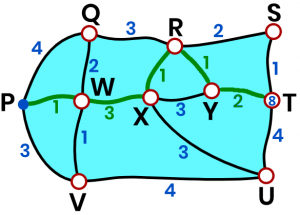 
`U` `:` `7` or `6`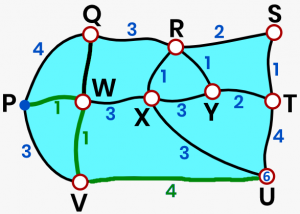 
Finally, fill in the table with the values of the shortest paths.`\text(From)` `P` `\text(To)` `Q` `3` `R` `5` `S` `7` `T` `8` `U` `6` `V` `2` `W` `1` `X` `4` `Y` `6` -
-
Question 3 of 4
3. Question
The network show the value in thousand dollars for putting up fiber optic cables to each location. Find the cost of putting up a cable from `A` to `D`
- `$` (29000)
Hint
Help VideoCorrect
Keep Going!
Incorrect
Dijkstra’s Algorithm is a method of finding a shortest path from a vertex to another by comparing multiple paths and finding the shortest value or sum of values.First, start finding the shortest paths to the vertices one edge away from `A`, which are `F`, `E`, and `B`.Always check for multiple paths and find the one with the lowest value.`F` `:` `16` or `12` 
`E` `:` `17` or `16` 
`B` `:` `15, 16` or `10` 
Now start finding the shortest paths to the vertices two edges away from `A`, which are `G` and `C`.Always check for multiple paths and find the one with the lowest value.`G` `:` `26, 26, 27` or `24` 
`C` `:` `29` or `24` 
Now start finding the paths to vertex `D`.Always check for multiple paths and find the one with the lowest value.`D` `:` `33, 32` or `29` 
Take note that each value in the network represents a thousand dollars.Therefore, a connection from `A` to `D` will cost `$29000`.`$29000` -
Question 4 of 4
4. Question
The network shows the flights around New South Wales with the cost listed in dollars. What is the cheapest rate to fly from Sydney to Dubbo?
- `$` (600)
Hint
Help VideoCorrect
Fantastic!
Incorrect
Dijkstra’s Algorithm is a method of finding a shortest path from a vertex to another by comparing multiple paths and finding the shortest value or sum of values.Try out multiple paths that will travel from Sydney to Dubbo and find the one with the least cost.`\text(Sydney-Woollongong-Wagga Wagga-Dubbo)` `:` `$610` 
`\text(Sydney-Bathurst-Dubbo)` `:` `$610` 
`\text(Sydney-Dubbo)` `:` `$610` 
`\text(Sydney-Tamworth-Dubbo)` `:` `$630` 
`\text(Sydney-Coffs Harbour-Tamworth-Dubbo)` `:` `$600` 
Therefore, the cheapest flight to take to get from Sydney to Dubbo will cost `$600`.`$600`
Quizzes
- Vertices and Edges
- Degrees 1
- Degrees 2
- Degrees 3
- Drawing a Network 1
- Drawing a Network 2
- Completing a Table from a Network Diagram
- Network from Maps and Plans
- Identify Paths and Cycles
- Eulerian Trails and Circuits 1
- Eulerian Trails and Circuits 2
- Identify Spanning Trees
- Minimum Spanning Trees 1
- Minimum Spanning Trees 2
- Shortest Path 1
- Shortest Path 2