Topics
>
Algebra 1>
Systems of Equations>
Systems of Nonlinear Equations>
Systems of Nonlinear EquationsSystems of Nonlinear Equations
Try VividMath Premium to unlock full access
Time limit: 0
Quiz summary
0 of 5 questions completed
Questions:
- 1
- 2
- 3
- 4
- 5
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
Loading...
- 1
- 2
- 3
- 4
- 5
- Answered
- Review
-
Question 1 of 5
1. Question
Find the solution to the system of equations by graphing.
`y=4-x^2`
`y=x^2-4`
- Intersection Point `1=` (2,0, -2,0) Intersection Point `2=` (2,0, -2,0)
Correct
Great Work!
Incorrect
First set the two equations equal to each other and solve for `x``x^2-4 \ color(crimson)(+x^2)` `=` `4-x^2 \ color(crimson)(+x^2)` Add `x^2` to both sides `-4 \ color(crimson)(+x^2+x^2)` `=` `4 \ cancel(-x^2+x^2)` `2x^2-4` `=` `4` `2x^2-4 \ color(crimson)(-4)` `=` `4 \ color(crimson)(-4)` Add `-4` to both sides `2x^2-8` `=` `0` Factor out a `2` `2(x^2-4)` `=` `0` `2(x-2)(x+2)` `=` `0` Factor using the difference of squares Solve `x-2` for `x`.`x-2` `=` `0` Solve for `x` `x` `=` `2` `y` `=` `(2)^2-4` Solve for the `y` coordinate by substituting `x=2` into the second equation `y=x^2-4` `y` `=` `0` The first solution is the point `(2,0)`Now solve `x+2` for `x`.`x+2` `=` `0` Solve for `x` `x` `=` `-2` `y` `=` `4-(-2)^2` Solve for the `y` coordinate by substituting `x=-2` into the first equation `y=4-x^2` `y` `=` `0` The second solution is the point `(-2,0)``:. color(darkviolet){(2,0)}` and ` color(darkviolet){(-2,0)}``(2,0)` and `(-2,0)` -
Question 2 of 5
2. Question
Find the solution to the system of equations by graphing.
`y=3x-2`
`y=x^2`
- Intersection Point `1=` (2,4, 1,1) Intersection Point `2=` (2,4, 1,1)
Correct
Great Work!
Incorrect
First set the two equations equal to each other and solve for `x``x^2 \ color(crimson)(-3x)` `=` `3x-2 \ color(crimson)(-3x)` Add `-3x` to both sides `x^2\ color(crimson)(-3x)` `=` `-2 \ cancel(+3x) cancel(-3x)` `x^2-3x` `=` `-2` `x^2-3x \ color(crimson)(+2)` `=` `-2 \ color(crimson)(+2)` Add `2` to both sides `x^2-3x+2` `=` `0` `(x-2)(x-1)` `=` `0` Factor Solve `x-2` for `x`.`x-2` `=` `0` Solve for `x` `x` `=` `2` `y` `=` `(2)^2` Solve for the `y` coordinate by substituting `x=2` into the second equation `y=x^2` `y` `=` `4` The first solution is the point `(2,4)`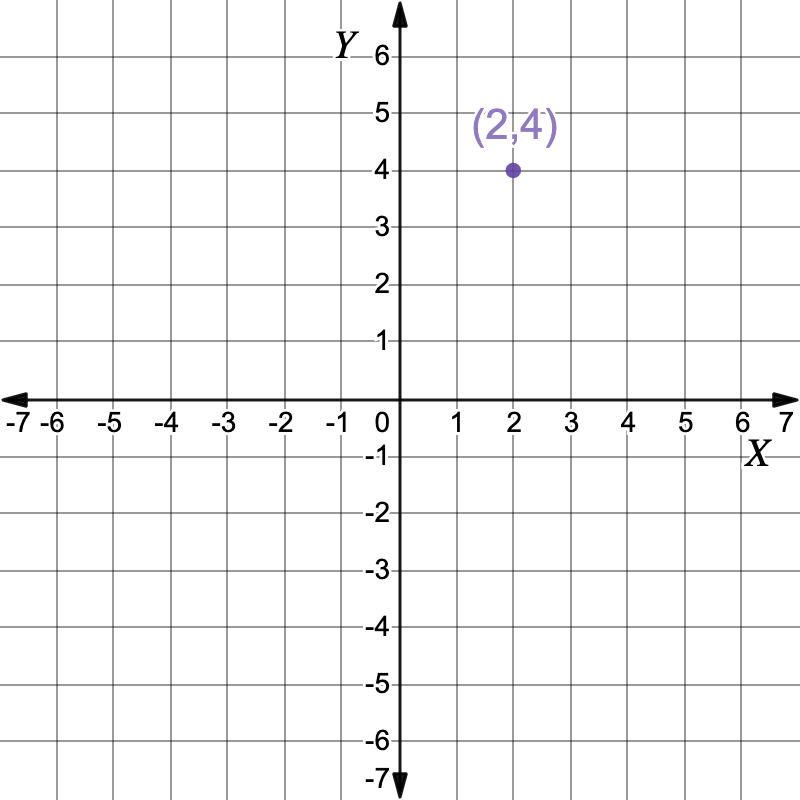 Now solve `x-1` for `x`.
Now solve `x-1` for `x`.`x-1` `=` `0` Solve for `x` `x` `=` `1` `y` `=` `(1)^2` Solve for the `y` coordinate by substituting `x=1` into the second equation `y=x^2` `y` `=` `1` The second solution is the point `(1,1)`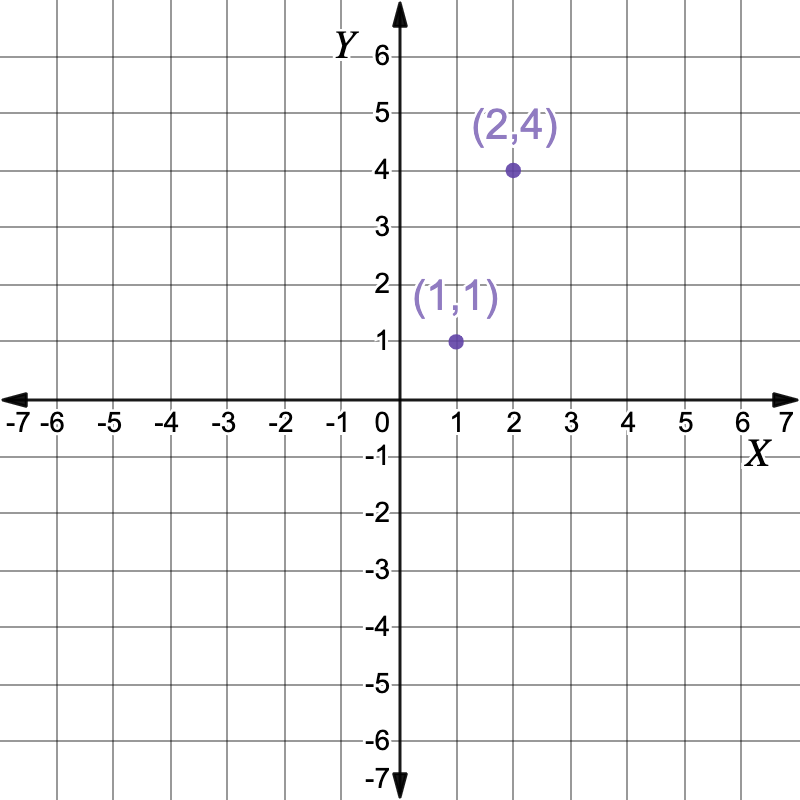 `:. color(darkviolet){(2,4)}` and ` color(darkviolet){(1,1)}``(2,4)` and `(1,1)`
`:. color(darkviolet){(2,4)}` and ` color(darkviolet){(1,1)}``(2,4)` and `(1,1)` -
Question 3 of 5
3. Question
Find the solution to the system of equations by graphing.
`y=-x-6`
`y=x^2-5x-3`
- Intersection Point `1=` (3,-9, 1,-7) Intersection Point `2=` (3,-9, 1,-7)
Correct
Great Work!
Incorrect
First set the two equations equal to each other and solve for `x``x^2-5x-3 \ color(crimson)(+x)` `=` `-x-6 \ color(crimson)(+x)` Add `x` to both sides `x^2-3 \ color(crimson)(-5x+x)` `=` `-6 \ cancel(-x) cancel(+x)` `x^2-4x-3` `=` `-6` `x^2-4x-3 \ color(crimson)(+6)` `=` `4 \ color(crimson)(+6)` Add `6` to both sides `x^2-4x+3` `=` `0` `(x-3)(x-1)` `=` `0` Factor Solve `x-3` for `x`.`x-3` `=` `0` Solve for `x` `x` `=` `3` `y` `=` `-(3)-6` Solve for the `y` coordinate by substituting `x=3` into the first equation `y=-x-6` `y` `=` `-9` The first solution is the point `(3,-9)`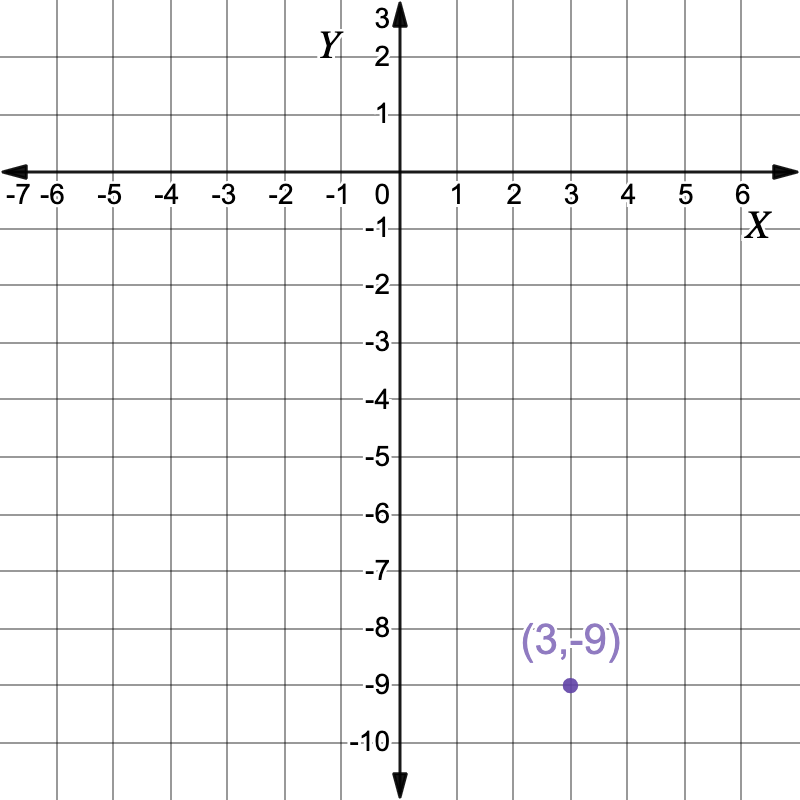 Now solve `x-1` for `x`.
Now solve `x-1` for `x`.`x-1` `=` `0` Solve for `x` `x` `=` `1` `y` `=` `-(1)-6` Solve for the `y` coordinate by substituting `x=1` into the first equation `y=-x-6` `y` `=` `-7` The second solution is the point `(1,-7)`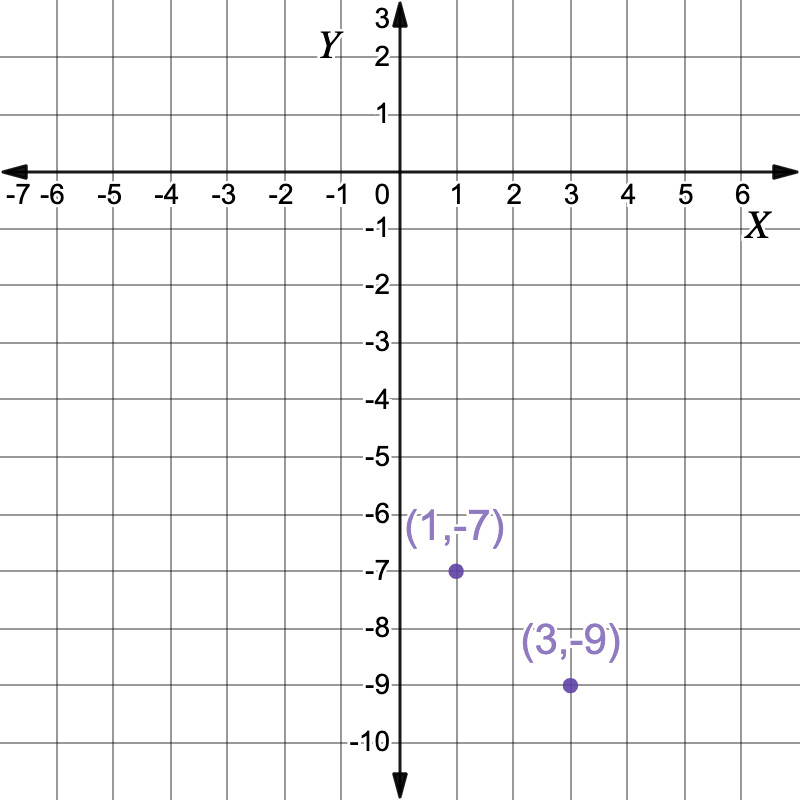 `:. color(darkviolet){(3,-9)}` and ` color(darkviolet){(1,-7)}``(3,-9)` and `(1,-7)`
`:. color(darkviolet){(3,-9)}` and ` color(darkviolet){(1,-7)}``(3,-9)` and `(1,-7)` -
Question 4 of 5
4. Question
Solve for `y`.`y=4x^2-6x``y=2x`-
`x_1 =` (0, 2)`x_2 =` (2, 0)`y_1 =` (0, 4)`y_2 =` (4, 0)
Hint
Help VideoCorrect
Well Done!
Incorrect
First, label the two equations `1` and `2` respectively.`y` `=` `4x^2-6x` Equation `1` `y` `=` `2x` Equation `2` Set Equations `1` and `2` equal to each other.`4x^2-6x` `=` `2x` `4x^2-6x``-2x` `=` `2x``-2x` Subtract `2x` from both sides `4x^2-8x` `=` `0` Simplify `4x(x-2)` `=` `0` Factor out `4x` from the left side Solve for `x``4``x` `=` `0` `x` `=` `0` `x``-2` `=` `0` `x``-2``+2` `=` `0``+2` `x` `=` `2` Now, substitute the value of `x` to solve for `y``y` `=` `2``x` `y` `=` `2``(0)` `x=0` `y` `=` `0` `y` `=` `2``x` `y` `=` `2``(2)` `x=2` `y` `=` `4` `x=0,2; y =0,4` -
-
Question 5 of 5
5. Question
Solve for `y`.`y=6x-3``y=x^2-8x+46`-
`x =` (7)`y =` (39)
Hint
Help VideoCorrect
Exceptional!
Incorrect
First, label the two equations `1` and `2` respectively.`y` `=` `6x-3` Equation `1` `y` `=` `x^2-8x+46` Equation `2` Set Equations `1` and `2` equal to each other.`6x-3` `=` `x^2-8x+46` `6x-3``-6x+3` `=` `x^2-8x+46``-6x+3` Add `-6x+3` to both sides `0` `=` `x^2-14x+49` Simplify `x^2-14x+49` `=` `0` Since the equation is in standard form `(``a``x^2+``b``x+``c``=0)` we can factorise using the cross method.`x^2``-14``x+``49``=0`To factorise, we need to find two numbers that add to `-14` and multiply to `49`Two `-7`’s fit both conditions`-7 + (-7)` `=` `-14` `-7 xx -7` `=` `49` Read across to get the factors.`(x-7)(x-7)=0`Solve for `x`.`x``-7` `=` `0` `x``-7``+7` `=` `0``+7` `x` `=` `7` Now, substitute the value of `x` to solve for `y``y` `=` `6``x``-3` `y` `=` `6``(7)``-3` `x=7` `y` `=` `42-3` `y` `=` `39` `x=7; y =39` -
Quizzes
- Solve a System of Equations by Graphing
- Substitution Method 1
- Substitution Method 2
- Substitution Method 3
- Substitution Method 4
- Elimination Method 1
- Elimination Method 2
- Elimination Method 3
- Elimination Method 4
- Systems of Nonlinear Equations
- Systems of Equations Word Problems 1
- Systems of Equations Word Problems 2









