hacklink hack forum hacklink film izle hacklink hd porno deneme bonusu veren siteler deneme bonusu veren siteler 2025 jojobet บาคาร่า สล็อตเว็บตรง สล็อตเว็บตรง sahabet vozol elektronik sigara tipobet tipobet betpuan 1xbet casibom tipobet tipobet atlasbet jojobet Vbet jojobet jojobet jojobet hacklink hacklink สล็อตเว็บตรง mavibet betoffice ultrabet güncel giriş casibom jojobet giriş romabet tipobet holiganbet matbet güncel giriş jojobet Grandpashabet betoffice matbet fixbet giriş casibom trendbet casibom casibom casibom nitrobahis Marsbahis Casibom sekabet Dinamobet Vdcasino betpuan Marsbahis jojobet betoffice betkolik betsmove giriş galabet deneme bonusu veren siteler pusulabet parmabet betovis casibom casibom artemisbet vaycasino giriş casibom jojobet giriş kavbet casibom bettilt holiganbet giriş betpark gamdom türkiye grandpashabet

Topics

>

>

>

Using Bearings to Find Distance

>

Using Bearings to Find Distance 2

Using Bearings to Find Distance 2

Try VividMath Premium to unlock full access

Start Free Trial

Loading...

Lets see your results!

Points

Score

Time

1
2
3
4

Answered
Review

Question 1 of 4

A ship has traveled

68 km

$68 \text(km)$ northwest from point

P

$P$ with a true bearing of

319 ° T

$319°T$ . How far west (

x_{w}

$x_w$ ) has it traveled?

Round your answer to one decimal place

$x_{w} =$ $x_w=$ (44.6) $km$ $\text(km)$

Incorrect

Need Text

Swarmify Video Hosting

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

Sin Ratio

s i n = \frac{opposite}{hypotenuse}

$sin=\frac{\color{#004ec4}{\text{opposite}}}{\color{#e85e00}{\text{hypotenuse}}}$

Cos Ratio

c o s = \frac{adjacent}{hypotenuse}

$cos=\frac{\color{#00880a}{\text{adjacent}}}{\color{#e85e00}{\text{hypotenuse}}}$

Tan Ratio

t a n = \frac{opposite}{adjacent}

$tan=\frac{\color{#004ec4}{\text{opposite}}}{\color{#00880a}{\text{adjacent}}}$

A true bearing is an angle measured clockwise from the True North around to the required direction.

First, find the value of

θ

$theta$ below.

Notice that it is part of the given bearing, which also consists of

3

$3$ quadrants from the North line moving clockwise.

To find the value of

θ

$theta$ , simply subtract the measure of the angles from the three quadrants,

270 °

$270°$ , from the given bearing.

$θ$ $theta$	$=$ $=$	$319 ° - 270 °$ $319°-270°$
	$=$ $=$	$49 °$ $49°$

To solve for $x_{w}$ $x_w$ , we can use the known values of the hypotenuse and

θ = 49 °

$thet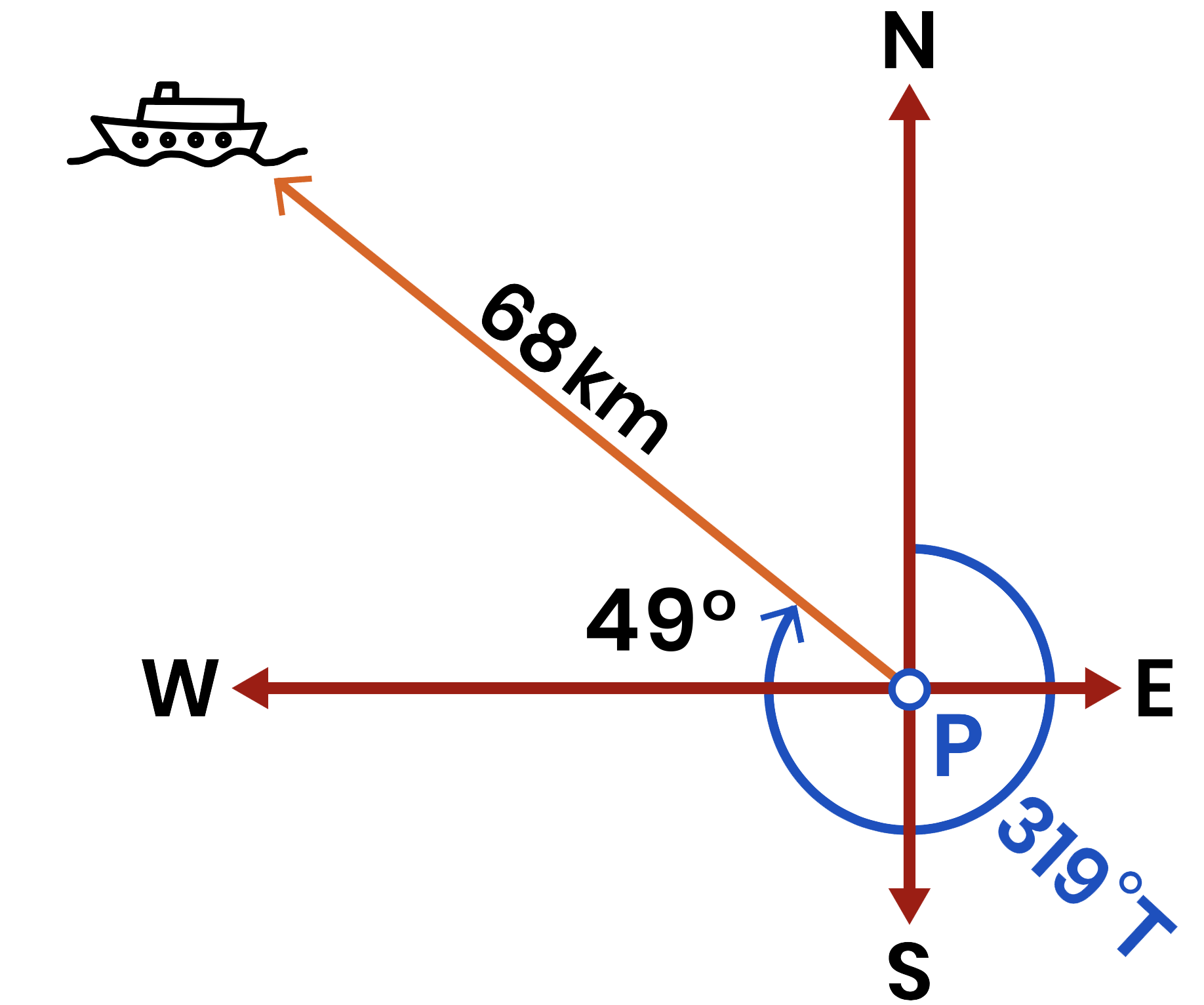a=49°$ .

Use

cos

$cos$ to find the value of $x_{w}$ $x_w$ .

$cos 49 °$ $cos49°$	$=$ $=$	$\frac{\color{#00880A}{x_w}}{\color{#e85e00}{\text{hypotenuse}}}$

$cos 49 °$ $cos49°$	$=$ $=$	$\frac{\color{#00880A}{x_w}}{\color{#e85e00}{68}}$

$cos 49 °$ $cos49°$ $\times 68$ $xx68$	$=$ $=$	$(\frac{x_{w}}{68})$ $((x_w)/68)$ $\times 68$ $xx68$	Multiply both sides by $68$ $68$

$68 cos 49 °$ $68cos49°$	$=$ $=$	$x_{w}$ $x_w$
$x_{w}$ $x_w$	$=$ $=$	$68 cos 49 °$ $68cos49°$

Using your calculator,

68 cos 49 ° = 44.6

$68cos49°=44.6$ .

Therefore, the speedboat is

44.6 km

$44.6 \text(km)$ to the West.

x_{w} = 44.6 km

$x_w=44.6 \text(km)$

Question 2 of 4

A marathon runner runs

25.3 km

$25.3 \text(km)$ at a true bearing of

129 ° T

$129°T$ . Find how far east (

x_{e}

$x_e$ ) the runner has traveled from the starting point (

S

$S$ ).

Round your answer to one decimal place

$x_{e} =$ $x_e=$ (19.7) $km$ $\text(km)$

Incorrect

Need Text

Swarmify Video Hosting

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

Sin Ratio

s i n = \frac{opposite}{hypotenuse}

$sin=\frac{\color{#004ec4}{\text{opposite}}}{\color{#e85e00}{\text{hypotenuse}}}$

Cos Ratio

c o s = \frac{adjacent}{hypotenuse}

$cos=\frac{\color{#00880a}{\text{adjacent}}}{\color{#e85e00}{\text{hypotenuse}}}$

Tan Ratio

t a n = \frac{opposite}{adjacent}

$tan=\frac{\color{#004ec4}{\text{opposite}}}{\color{#00880a}{\text{adjacent}}}$

A true bearing is an angle measured clockwise from the True North around to the required direction.

First, find the value of

θ

$theta$ below.

Notice that it is part of the given bearing, which also consists of a right angle from the North line moving to the East line.

To find the value of

θ

$theta$ , simply subtract the value of a right angle,

90 °

$90°$ , from the given bearing.

$θ$ $theta$	$=$ $=$	$129 ° - 90 °$ $129°-90°$
	$=$ $=$	$39 °$ $39°$

To solve for $x_{e}$ $x_e$ , we can use the known values of the hypotenuse and

θ = 39 °

$theta=39°$ .

Use

cos

$cos$ to find the value of $x_{e}$ $x_e$ .

$cos 39 °$ $cos39°$	$=$ $=$	$\frac{\color{#00880A}{x_e}}{\color{#e85e00}{\text{hypotenuse}}}$

$cos 39 °$ $cos39°$	$=$ $=$	$\frac{\color{#00880A}{x_e}}{\color{#e85e00}{25.3}}$

$cos 39 °$ $cos39°$ $\times 25.3$ $xx25.3$	$=$ $=$	$(\frac{x_{e}}{25.3})$ $((x_e)/25.3)$ $\times 25.3$ $xx25.3$	Multiply both sides by $25.3$ $25.3$

$25.3 cos 39 °$ $25.3cos39°$	$=$ $=$	$x_{e}$ $x_e$
$x_{e}$ $x_e$	$=$ $=$	$25.3 cos 39 °$ $25.3cos39°$

Using your calculator,

25.3 cos 39 ° = 19.7

$25.3cos39°=19.7$ .

Therefore, the runner runs

19.7 km

$19.7 \text(km)$ to the East.

x_{e} = 19.7 km

$x_e=19.7 \text(km)$

Question 3 of 4

A ship sails on a bearing of

200 ° T

$200° T$ towards

P

$P$ . If

P

$P$ is

80

$80$ nautical miles west from

O

$O$ , find how far the ship has sailed

(x)

$(x)$ .

Round your answer to one decimal place

(233.9) $nautical miles$ $\text(nautical miles)$

Incorrect

Need Text

Swarmify Video Hosting

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

>

Sin Ratio

s i n = \frac{opposite}{hypotenuse}

$sin=\frac{\color{#004ec4}{\text{opposite}}}{\color{#e85e00}{\text{hypotenuse}}}$

Cos Ratio

c o s = \frac{adjacent}{hypotenuse}

$cos=\frac{\color{#00880a}{\text{adjacent}}}{\color{#e85e00}{\text{hypotenuse}}}$

Tan Ratio

t a n = \frac{opposite}{adjacent}

$tan=\frac{\color{#004ec4}{\text{opposite}}}{\color{#00880a}{\text{adjacent}}}$

A true bearing is an angle measured clockwise from the True North around to the required direction.

First, find the value of angle

Q O P

$QOP$ .

Notice that adding angle

Q O P

$QOP$ to the given bearing

(200 °)

$(200°)$ will cover

3

$3$ quadrants, which is equal to

270 °

$270°$

To find the value of angle $Q O P$ $QOP$ , simply subtract the value of the bearing from

270 °

$270°$ .

$∠ Q O P$ $/_QOP$	$=$ $=$	$270 ° - 200 °$ $270°-200°$
	$=$ $=$	$70 °$ $70°$

To solve for $x$ $x$ , we can use the known values of the line adjacent to angle $Q O P$ $QOP$ .

Use

cos

$cos$ to find the value of $x$ $x$ .

$cos 70 °$ $cos70°$	$=$ $=$	$\frac{\color{#00880A}{\text{adjacent}}}{\color{#e85e00}{x}}$

$cos 70 °$ $cos70°$	$=$ $=$	$\frac{\color{#00880A}{80}}{\color{#e85e00}{x}}$

$cos 70 °$ $cos70°$ $\times x$ $xxx$	$=$ $=$	$(\frac{80}{x})$ $((80)/x)$ $\times x$ $xxx$	Multiply both sides by $x$ $x$

$x cos 70 °$ $xcos70°$	$=$ $=$	$80$ $80$

$x cos 70 °$ $xcos70°$ $\div cos 70 °$ $divcos70°$	$=$ $=$	$80$ $80$ $\div cos 70 °$ $divcos70°$	Divide both sides by $cos 70 °$ $cos70°$
$x$ $x$	$=$ $=$	$\frac{80}{cos 70 °}$ $(80)/(cos70°)$

Using your calculator,

\frac{80}{cos 70 °} = 233.9

$(80)/(cos70°)=233.9$ .

Therefore, the boat traveled

233.9 nautical miles

$233.9 \text(nautical miles)$ in total.

233.9 nautical miles

$233.9 \text(nautical miles)$

Question 4 of 4

Bianca leaves her home and cycles due North for

12

$12$ km, then

7

$7$ km due West to go to the gym. How far is the gym from her home

(x)

$(x)$ ?

Round your answer to one decimal place

(13.9) $km$ $\text(km)$