Working with Radial Surveys 3

Topics

Trigonometry

Bearings

Radial Surveys

Working with Radial Surveys 3

Try VividMath Premium to unlock full access

Start Free Trial

Lets see your results!

Points

Score

Time

Retry Quiz

Answered
Review

Question 1 of 5

1. Question
From the radial survey below, find $∠ P O Q$ $angle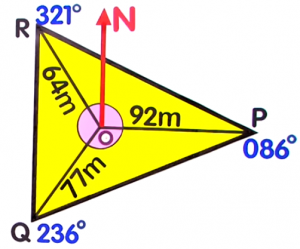POQ$ :
- $∠ P O Q =$ $anglePOQ=$ (150) $°$ $°$
Hint

Help Video
Correct

Excellent!
Incorrect
Need Text
Play
Current Time 0:00
/
Duration Time 0:00
Remaining Time -0:00
Stream TypeLIVE
Loaded: 0%
Progress: 0%
0:00
Fullscreen
Video Acceleration:
On
Off

00:00
Mute
Playback Rate
1x
2x
1.5x
1.25x
1x
0.75x
0.5x
Subtitles
subtitles off
Captions
captions off
English
Chapters
Chapters

A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.

Notice that $∠ P O Q$ $anglePOQ$ is the difference between the bearings of $P$ $P$ and $Q$ $Q$ .

Subtract the bearing of $P$ $P$ from the bearing of $Q$ $Q$ .

$∠ P O Q$ $anglePOQ$ $=$ $=$ $∠ Q - ∠ P$ $angleQ-angleP$

$=$ $=$ $236 ° - 86 °$ $236°-86°$ Substitute the values

$=$ $=$ $150 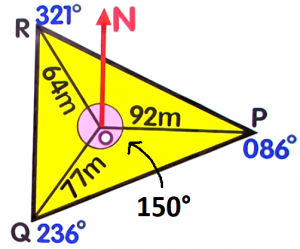°$ $150°$

$150 °$ $150°$
Question 2 of 5

2. Question
From the radial survey below, find $∠ R O Q$ $angleROQ$ :
- $∠ R O Q =$ $angleROQ=$ (85) $°$ $°$
Hint

Help Video
Correct

Correct!
Incorrect
Need Text
Play
Current Time 0:00
/
Duration Time 0:00
Remaining Time -0:00
Stream TypeLIVE
Loaded: 0%
Progress: 0%
0:00
Fullscreen
Video Acceleration:
On
Off

00:00
Mute
Playback Rate
1x
2x
1.5x
1.25x
1x
0.75x
0.5x
Subtitles
subtitles off
Captions
captions off
English
Chapters
Chapters

A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.

Notice that $∠ R O Q$ $angleROQ$ is the difference between the bearings of $Q$ $Q$ and $R$ $R$ .

Subtract the bearing of $Q$ $Q$ from the bearing of $R$ $R$ .

$∠ R O Q$ $angleROQ$ $=$ $=$ $∠ R - ∠ Q$ $angleR-angleQ$

$=$ $=$ $321 ° - 236 °$ $321°-236°$ Substitute the values

$=$ $=$ $85 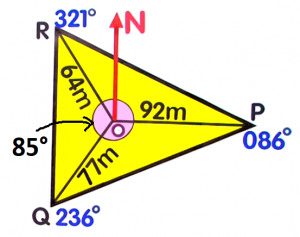°$ $85°$

$85 °$ $85°$
Question 3 of 5

3. Question
From the radial survey below, find $∠ R O P$ $angleROP$ :
- $∠ R O P =$ $angleROP=$ (125) $°$ $°$
Hint

Help Video
Correct

Great Work!
Incorrect
Need Text
Play
Current Time 0:00
/
Duration Time 0:00
Remaining Time -0:00
Stream TypeLIVE
Loaded: 0%
Progress: 0%
0:00
Fullscreen
Video Acceleration:
On
Off

00:00
Mute
Playback Rate
1x
2x
1.5x
1.25x
1x
0.75x
0.5x
Subtitles
subtitles off
Captions
captions off
English
Chapters
Chapters

A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.

Since $∠ R O P$ $angleROP$ is the sum of $∠ R O N$ $angleRON$ and $∠ N O P$ $angleNOP$ , start with solving for $∠ R O N$ $angleRON$ .

Knowing that a full revolution from $N$ $N$ measures $360 °$ $360°$ , subtract the bearing of $R$ $R$ to get $∠ R O N$ $angleRON$

$∠ R O N$ $angleRON$ $=$ $=$ $360 ° - ∠ R$ $360°-angleR$

$=$ $=$ $360 ° - 321 °$ $360°-321°$ Substitute the values

$=$ $=$ $39 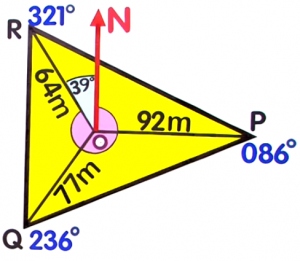°$ $39°$

Finally, proceed with adding $∠ R O N$ $angleRON$ and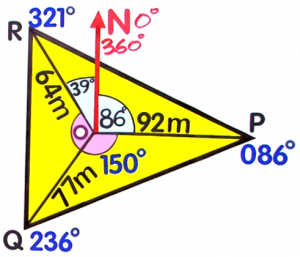 $∠ N O P$ $angleNOP$ .

$∠ R O P$ $angleROP$ $=$ $=$ $∠ R O N + ∠ N O P$ $angleRON+angleNOP$

$=$ $=$ $39 ° + 86 °$ $39°+86°$ Substitute the values

$=$ $=$ $125 °$ $125°$

$125 °$ $125°$

Question 4 of 5

From the radial survey below, find the area of

△ P O Q

$trianglePOQ$ :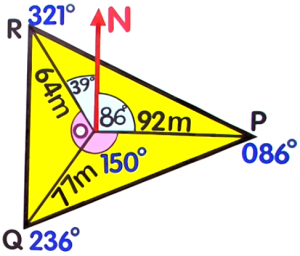

Area of $△ P O Q =$ $trianglePOQ=$ (1771) $m^{2}$ $m^2$

Incorrect

Need Text

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

Area of a Non-Right Angled Triangle

A_{△} = \frac{1}{2}

$A_triangle=1/2$ $a$ $a$ $b$ $b$

\sin

$sin$ $C$ $C$

where:
$a$ $a$ is the side opposite angle $A$ $A$
$b$ $b$ is the side opposite angle $B$ $B$
$c$ $c$ is the side opposite angle $C$ $C$

A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.

First, identify the known values of the triangle

P O Q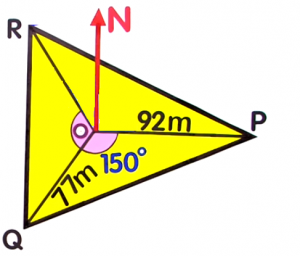

$POQ$ .

Now, substitute the known values to the formula and solve for the area.

a = 77 m

$a=77m$

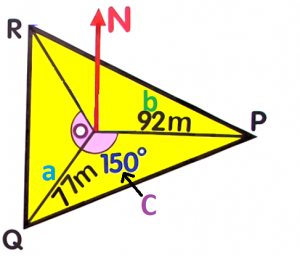b = 92 m

$b=92m$

C = 150 °

$C=150°$

$A_{△}$ $A_triangle$	$=$ $=$	$\frac{1}{2}$ $1/2$ $a$ $a$ $b$ $b$ $\sin$ $sin$ $C$ $C$

	$=$ $=$	$\frac{1}{2} ($ $1/2($ $77$ $77$ $) ($ $)($ $92$ $92$ $) \sin$ $)sin$ $150 °$ $150°$	Substitute the values

	$=$ $=$	$3542 \times \sin 150 °$ $3542timessin150°$	Evaluate $\sin$ $sin$ $150$ $150$ on your calculator

	$=$ $=$	$1771 m^{2}$ $1771m^2$

1771 m^{2}

$1771m^2$

Question 5 of 5

From the radial survey below, find the area of

△ Q O R

$triangleQOR$ :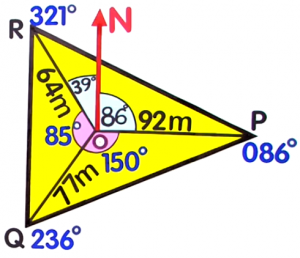

Round off to

2

$2$ decimal places

Area of $△ Q O R =$ $triangleQOR=$ (2454.62) $m^{2}$ $m^2$

Incorrect

Need Text

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

Area of a Non-Right Angled Triangle

A_{△} = \frac{1}{2}

$A_triangle=1/2$ $a$ $a$ $b$ $b$

\sin

$sin$ $C$ $C$

where:
$a$ $a$ is the side opposite angle $A$ $A$
$b$ $b$ is the side opposite angle $B$ $B$
$c$ $c$ is the side opposite angle $C$ $C$

A radial survey is a tool used for land and seafloor mapping. Each corner of the area being measured is connected to a central point.

First, identify the known values of the triangle

Q O R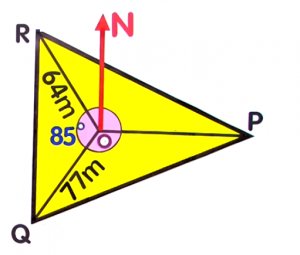

$QOR$ .

Now, substitute the known values to the formula and solve for the area.

a = 64 m

$a=64m$

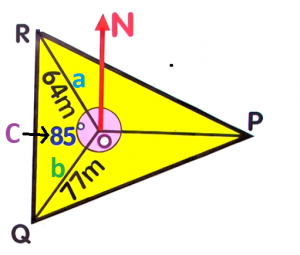b = 77 m

$b=77m$

C = 85 °

$C=85°$

$A_{△}$ $A_triangle$	$=$ $=$	$\frac{1}{2}$ $1/2$ $a$ $a$ $b$ $b$ $\sin$ $sin$ $C$ $C$

	$=$ $=$	$\frac{1}{2} ($ $1/2($ $64$ $64$ $) ($ $)($ $77$ $77$ $) \sin$ $)sin$ $85 °$ $85°$	Evaluate $\sin$ $sin$ $85$ $85$ on your calculator

	$=$ $=$	$2464 \times 0.9961947$ $2464times0.9961947$	Simplify
	$=$ $=$	$2454.6237408$ $2454.6237408$
	$=$ $=$	$2454.62 m^{2}$ $2454.62m^2$	Round off to $2$ $2$ decimal places

2454.62 m^{2}

$2454.62m^2$

Working with Radial Surveys 3

Try VividMath Premium to unlock full access

Quiz summary

Information

1. Question

Hint

Excellent!

2. Question

Hint

Correct!

3. Question

Hint

Great Work!

4. Question

Hint

Good Job!

Area of a Non-Right Angled Triangle

5. Question

Hint

Fantastic!

Area of a Non-Right Angled Triangle

Quizzes

$∠ P O Q$ $anglePOQ$	$=$ $=$	$∠ Q - ∠ P$ $angleQ-angleP$
	$=$ $=$	$236 ° - 86 °$ $236°-86°$	Substitute the values
	$=$ $=$	$150 °$ $150°$

$∠ R O Q$ $angleROQ$	$=$ $=$	$∠ R - ∠ Q$ $angleR-angleQ$
	$=$ $=$	$321 ° - 236 °$ $321°-236°$	Substitute the values
	$=$ $=$	$85 °$ $85°$

$∠ R O N$ $angleRON$	$=$ $=$	$360 ° - ∠ R$ $360°-angleR$
	$=$ $=$	$360 ° - 321 °$ $360°-321°$	Substitute the values
	$=$ $=$	$39 °$ $39°$

$∠ R O P$ $angleROP$	$=$ $=$	$∠ R O N + ∠ N O P$ $angleRON+angleNOP$
	$=$ $=$	$39 ° + 86 °$ $39°+86°$	Substitute the values
	$=$ $=$	$125 °$ $125°$