Surface Area of Shapes 2

Question 1 of 7

Find the surface area of the figure

Round your answer to two decimal places

$Surface Area =$ $\text(Surface Area )=$ (617.92) ${cm}^{2}$ $\text(cm)^2$

Incorrect

Need Text

Play

Remaining Time -0:00

Stream TypeLIVE

Loaded: 0%

Progress: 0%

0:00

Fullscreen

00:00

Mute

Area of a Triangle Formula

Area = \frac{1}{2} \times

$\text(Area )=1/2 times$ $base$ $\text(base)$

\times

$times$ $height$ $\text(height)$

Area of a Rectangle Formula

Area =

$\text(Area )=$ $length$ $\text(length)$

\times

$times$ $height$ $\text(height)$

Showing and Labelling the Surfaces

We need to add the areas of all the faces of the figure: the two triangles and the three rectangles

First, to find the area of the triangle, get the height that is perpendicular to its base.

Label the sides of the right triangle formed within a triangle

Use the Pythagorean Theorem Formula to solve for $a$ $a$ , which is equal to the $height$ $\text(height)$

$a^{2}$ $a^2$ $+$ $+$ $b^{2}$ $b^2$	$=$ $=$	$c^{2}$ $c^2$	Pythagoras’ Theorem Formula
$h^{2}$ $\text(h)^2$ $+$ $+$ $4^{2}$ $4^2$	$=$ $=$	$7^{2}$ $7^2$	Plug in the known lengths
$h^{2} + 16$ $\text(h)^2+16$	$=$ $=$	$49$ $49$	Evaluate $4^{2}$ $4^2$ and $7^{2}$ $7^2$
$h^{2}$ $\text(h)^2$	$=$ $=$	$33$ $33$	Subtract $16$ $16$ from both sides
$height$ $\text(height)$	$=$ $=$	$5.74 cm$ $5.74 \text(cm)$	Take the square root of both sides

Next, solve for the area of the triangles using the Area of a Triangle formula

Note that there are two triangles with the same lengths, so we will multiply this area by

2

$2$ for the surface area

$Area$ $\text(Area)$ _{$triangles$ $\text(triangles)$}	$=$ $=$	$\frac{1}{2} \times$ $1/2 times$ $base$ $\text(base)$ $\times$ $times$ $height$ $\text(height)$

	$=$ $=$	$\frac{1}{2} \times$ $1/2 times$ $8$ $8$ $\times$ $times$ $5.74$ $5.74$ $=$ $=$ $22.96 {cm}^{2}$ $22.96 \text(cm)^2$

Now, solve for the area of the rectangles using the Area of a Rectangle formula

Note that there are two rectangles with the same lengths, so we will multiply the first area by

2

$2$ for the surface area

$Area$ $\text(Area)$ _{$equal rectangles$ $\text(equal rectangles)$}	$=$ $=$	$length$ $\text(length)$ $\times$ $times$ $height$ $\text(height)$
	$=$ $=$	$7$ $7$ $\times$ $times$ $26$ $26$ $=$ $=$ $182 {cm}^{2}$ $182 \text(cm)^2$

$Area$ $\text(Area)$ _{$middle rectangle$ $\text(middle rectangle)$}	$=$ $=$	$length$ $\text(length)$ $\times$ $times$ $height$ $\text(height)$
	$=$ $=$	$8$ $8$ $\times$ $times$ $26$ $26$ $=$ $=$ $208 {cm}^{2}$ $208 \text(cm)^2$

Finally, add all the areas to find the surface area of the figure

$SA$ $\text(SA)$	$=$ $=$	$(2 \times$ $(2times$ $22.96$ $22.96$ $) + (2 \times$ $)+(2times$ $182$ $182$ $) +$ $)+$ $208$ $208$	Plug in the areas
$SA$ $\text(SA)$	$=$ $=$	$617.92 {cm}^{2}$ $617.92 \text(cm)^2$

The given measurements are in centimetres, so the area is measured as square centimetres

SA = 617.92 {cm}^{2}

$\text(SA)=617.92 \text(cm)^2$

Question 2 of 7

What is the surface area of this Rectangular Prism?

Surface Area $=$ $=$ (320) $m m^{2}$ $mm^2$

Question 3 of 7

Find the surface area of the Cone

Round your answer to

1

$1$ decimal place

Use

π = 3.141592654

$pi=3.141592654$

$Surface Area =$ $\text(Surface Area )=$ (7710.7, 7706.8, 7713.8) ${cm}^{2}$ $\text(cm)^2$

Using	Answer
$π = 3.141592654$ $pi=3.141592654$	$7710.7 c m^{2}$ $7710.7 cm^2$
$π = 3.14$ $pi=3.14$	$7706.8 c m^{2}$ $7706.8 cm^2$
$π = \frac{22}{7}$ $pi=(22)/(7)$	$7713.8 c m^{2}$ $7713.8 cm^2$

Question 4 of 7

What is the surface area of this cone?

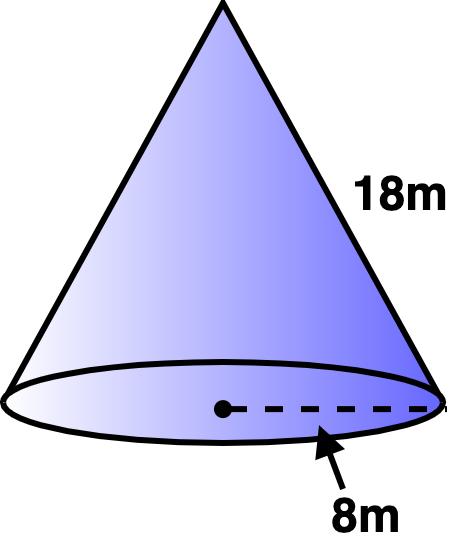Round your answer to

1

$1$ decimal place

Use

π \approx 3.14

$pi~~3.14$

Surface Area $=$ $=$ (653.1) $m^{2}$ $m^2$

Question 5 of 7

What is the surface area of this cone?

Use

π \approx 3.14

$pi~~3.14$

Surface Area $=$ $=$ (785) $m m^{2}$ $mm^2$

Question 6 of 7

Find the surface area of the Sphere

Round your answer to

1

$1$ decimal place

Use

π = 3.141592654

$pi=3.141592654$

$Surface Area =$ $\text(Surface Area )=$ (1520.5, 1519.8, 1521.1) ${cm}^{2}$ $\text(cm)^2$

Using	Answer
$π = 3.141592654$ $pi=3.141592654$	$1520.5 c m^{2}$ $1520.5 cm^2$
$π = 3.14$ $pi=3.14$	$1519.8 c m^{2}$ $1519.8 cm^2$
$π = \frac{22}{7}$ $pi=(22)/(7)$	$1521.1 c m^{2}$ $1521.1 cm^2$

Question 7 of 7

What is the surface area of this sphere?

Round your answer to

1

$1$ decimal place

Use

π \approx 3.14

$pi~~3.14$

Surface Area $=$ $=$ (615.4) $c m^{2}$ $cm^2$

$S A$ $SA$	$=$ $=$	$2 \times (width \times height + depth \times height + width \times depth)$ $2 xx (color(royalblue)(text(width)) xx color(green)(text(height)) + color(orange)(text(depth)) xx color(green)(text(height)) + color(royalblue)(text(width)) xx color(orange)(text(depth)))$	Surface area of a Rectangular Prism formula

	$=$ $=$	$2 \times (12 \times 7 + 4 \times 7 + 12 \times 4)$ $2 xx (color(royalblue)(text(12)) xx color(green)(text(7)) + color(orange)(text(4)) xx color(green)(text(7)) + color(royalblue)(text(12)) xx color(orange)(text(4)))$	Plug in the known lengths

	$=$ $=$	$320$ $320$	Simplify

	$=$ $=$	$320 m m^{2}$ $320 \ mm^2$

$S A$ $SA$	$=$ $=$	$π \times {radius}^{2} + π \times radius \times length$ $pi xx color(royalblue)(text(radius))^2+pi xx color(royalblue)(\text(radius)) xx color(darkviolet)(\text(length))$	Surface area of a cone formula

	$=$ $=$	$3.14 \times 8^{2} + 3.14 \times 8 \times 18$ $3.14 xx color(royalblue)(8)^2+3.14 xx color(royalblue)(8) xx color(darkviolet)(18)$	Plug in the known lengths

	$=$ $=$	$3.14 \times 64 + 3.14 \times 8 \times 18$ $3.14 xx 64+3.14 xx 8 xx 18$	Simplify
	$=$ $=$	$200.96 + 452.16$ $200.96 + 452.16$
	$=$ $=$	$653.1 m^{2}$ $653.1 \ m^2$	Rounded to 1 decimal place

$radius$ $color(royalblue)(text(radius))$	$=$ $=$	$\frac{1}{2} \times 20$ $1/2 xx color(forestgreen)(20)$

$radius$ $color(royalblue)(text(radius))$	$=$ $=$	$10$ $color(royalblue)(10)$

$S A$ $SA$	$=$ $=$	$π \times {radius}^{2} + π \times radius \times length$ $pi xx color(royalblue)(text(radius))^2+pi xx color(royalblue)(\text(radius)) xx color(darkviolet)(\text(length))$	Surface area of a cone formula

	$=$ $=$	$3.14 \times 10^{2} + 3.14 \times 10 \times 15$ $3.14 xx color(royalblue)(10)^2+3.14 xx color(royalblue)(10) xx color(darkviolet)(15)$	Plug in the known lengths

	$=$ $=$	$3.14 \times 100 + 3.14 \times 10 \times 15$ $3.14 xx 100+3.14 xx 10 xx 15$	Simplify
	$=$ $=$	$314 + 471$ $314+471$
	$=$ $=$	$785 m m^{2}$ $785 \ mm^2$

$radius$ $\text(radius)$	$=$ $=$	$\frac{1}{2} \times$ $1/2 times$ $22$ $22$

$radius$ $\text(radius)$	$=$ $=$	$11$ $11$

Surface Area of Shapes 2

Try VividMath Premium to unlock full access

Quiz summary

Information

1. Question

Hint

Correct!

Area of a Triangle Formula

Area of a Rectangle Formula

Showing and Labelling the Surfaces

2. Question

Keep Going!

Surface Area of a Rectangular Prism

Labelling the given lengths

3. Question

Hint

Correct!

Surface Area of a Closed Cone

Showing and Labelling the Surfaces

4. Question

Keep Going!

Surface Area of a Cone

Labelling the given lengths

5. Question

Keep Going!

Surface Area of a Cone

Labelling the given lengths

6. Question

Hint

Nice Job!

Surface Area of a Sphere

Showing and Labelling the Surfaces

7. Question

Keep Going!

Surface Area of a Sphere

Labelling the given lengths

Quizzes

$radius$ $\text(radius)$	$=$ $=$	$\frac{1}{2} \times$ $1/2 times$ $52$ $52$

$radius$ $\text(radius)$	$=$ $=$	$26$ $26$

$SA$ $\text(SA)$	$=$ $=$	$π \times$ $pi times$ ${radius}^{2}$ $\text(radius)^2$ $+ π \times$ $+pi times$ $radius$ $\text(radius)$ $\times$ $times$ $length$ $\text(length)$	Surface Area formula
$SA$ $\text(SA)$	$=$ $=$	$π \times$ $pi times$ $26^{2}$ $26^2$ $+ π \times$ $+pi times$ $26$ $26$ $\times$ $times$ $68.4$ $68.4$	Plug in the known lengths
$SA$ $\text(SA)$	$=$ $=$	$7710.725$ $7710.725$
$SA$ $\text(SA)$	$=$ $=$	$7710.7 {cm}^{2}$ $7710.7 \text(cm)^2$	Rounded to one decimal place

$SA$ $\text(SA)$	$=$ $=$	$4 \times π \times$ $4 times pi times$ ${radius}^{2}$ $\text(radius)^2$	Surface Area formula
$SA$ $\text(SA)$	$=$ $=$	$4 \times π \times$ $4 times pi times$ $11^{2}$ $11^2$	Plug in the known lengths
$SA$ $\text(SA)$	$=$ $=$	$1520.53084$ $1520.53084$
$SA$ $\text(SA)$	$=$ $=$	$1520.5 {cm}^{2}$ $1520.5 \text(cm)^2$	Rounded to one decimal place

$radius$ $color(royalblue)(text(radius))$	$=$ $=$	$\frac{1}{2} \times 14$ $1/2 xx color(forestgreen)(14)$

$radius$ $color(royalblue)(text(radius))$	$=$ $=$	$7$ $color(royalblue)(7)$

$S A$ $SA$	$=$ $=$	$4 \times π \times {radius}^{2}$ $4 xx pi xx color(royalblue)(text(radius))^2$	Surface area of a sphere formula

	$=$ $=$	$4 \times 3.14 \times 7^{2}$ $4 xx 3.14 xx color(royalblue)(7)^2$	Plug in the known lengths

	$=$ $=$	$4 \times 3.14 \times 49$ $4 xx 3.14 xx 49$	Simplify
	$=$ $=$	$615.44$ $615.44$
	$=$ $=$	$615.4 c m^{2}$ $615.4 \ cm^2$	Rounded to 1 decimal place