>
Algebra 2>
Radicals>
Rationalizing the Denominator using Conjugates>
Rationalizing the Denominator using ConjugatesRationalizing the Denominator using Conjugates
Get 3 days of unlimited access for free
No credit card required.
Quiz summary
0 of 4 questions completed
Questions:
- 1
- 2
- 3
- 4
Information
–
You have already completed the quiz before. Hence you can not start it again.
Quiz is loading...
You must sign in or sign up to start the quiz.
You have to finish following quiz, to start this quiz:
- 1
- 2
- 3
- 4
- Answered
- Review
-
Question 1 of 4
1. Question
Express the following with rational denominators:
`1/(2+sqrt2)`
Correct
Excellent!
Incorrect
Difference of Two Squares
`(a+b)(a-b)=a^2-b^2`The conjugate is where we change the sign in the middle of two terms like this:
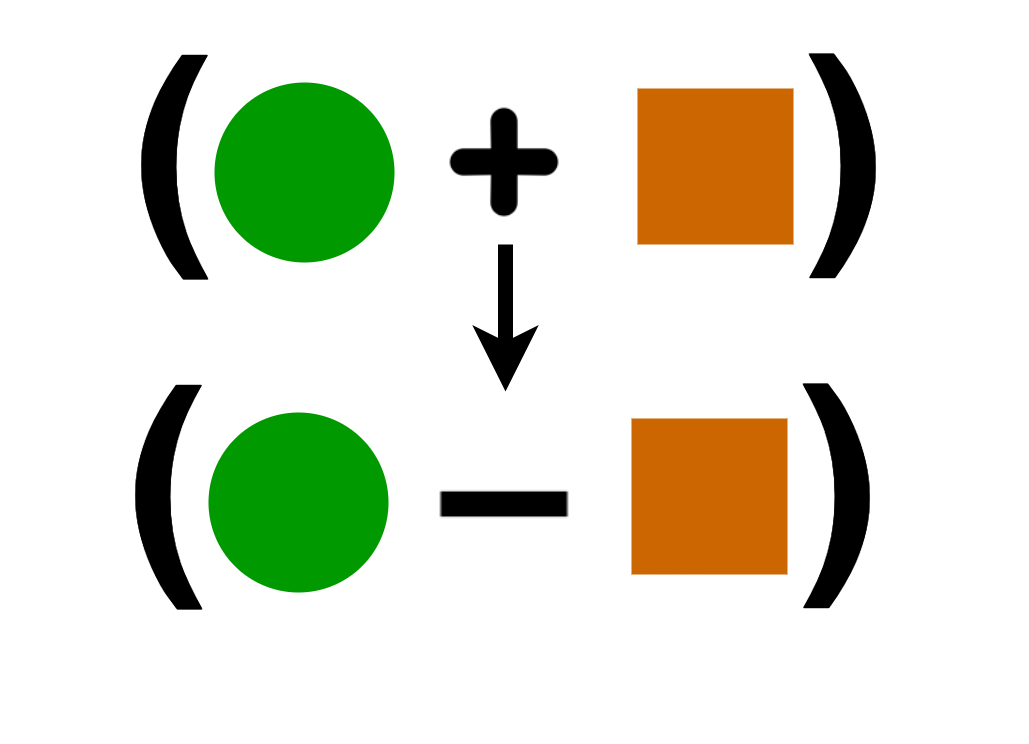 For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(2-sqrt2)`
For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(2-sqrt2)``1/(2+sqrt2)` `=` `1/(2+sqrt2) xx color(crimson)((2-sqrt2)/(2-sqrt2))` `=` `(2-sqrt2)/((2+sqrt2)(2-sqrt2))` Simplify using the difference of two squares `=` `(2-sqrt2)/((2)^2-(sqrt2)^2)` Simplify `=` `(2-sqrt2)/(4-2)` `(2)^2 = 4` and `(sqrt(2))^2 = 2` `=` `(2-sqrt2)/2` `(2-sqrt2)/2` -
Question 2 of 4
2. Question
Express the following with rational denominators:
`1/(sqrt6-sqrt5)`
Correct
Excellent!
Incorrect
Difference of Two Squares
`(a+b)(a-b)=a^2-b^2`The conjugate is where we change the sign in the middle of two terms like this:
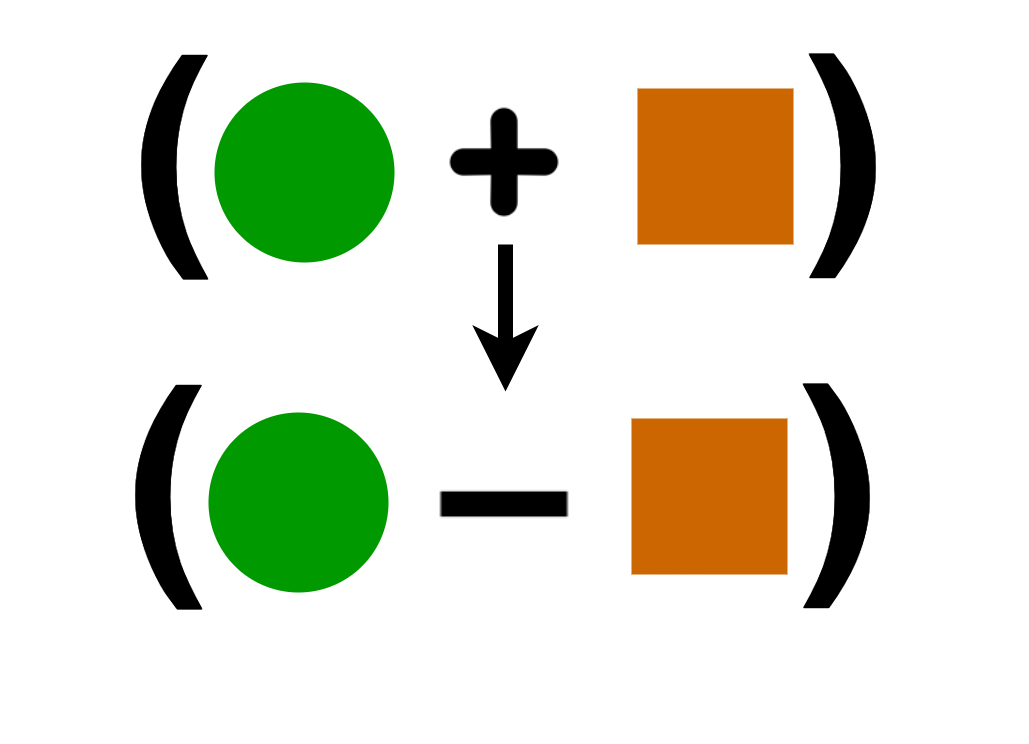 For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(sqrt6+sqrt5)`
For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(sqrt6+sqrt5)``1/(sqrt6-sqrt5)` `=` `1/(sqrt6-sqrt5) xx color(crimson)((sqrt6+sqrt5)/(sqrt6+sqrt5))` `=` `(sqrt6+sqrt5)/((sqrt6-sqrt5)(sqrt6+sqrt5))` Simplify using the difference of two squares `=` `(sqrt6+sqrt5)/((sqrt6)^2-(sqrt5)^2)` Simplify square roots `=` `(sqrt6+sqrt5)/(6-5)` `(sqrt(36))^2 = 6` and `(sqrt(25))^2 = 5` `=` `(sqrt6+sqrt5)/1` `=` `sqrt6+sqrt5` `sqrt6+sqrt5` -
Question 3 of 4
3. Question
Express the following with rational denominators:
`4/(4-sqrt2)`
Correct
Excellent!
Incorrect
Difference of Two Squares
`(a+b)(a-b)=a^2-b^2`The conjugate is where we change the sign in the middle of two terms like this:
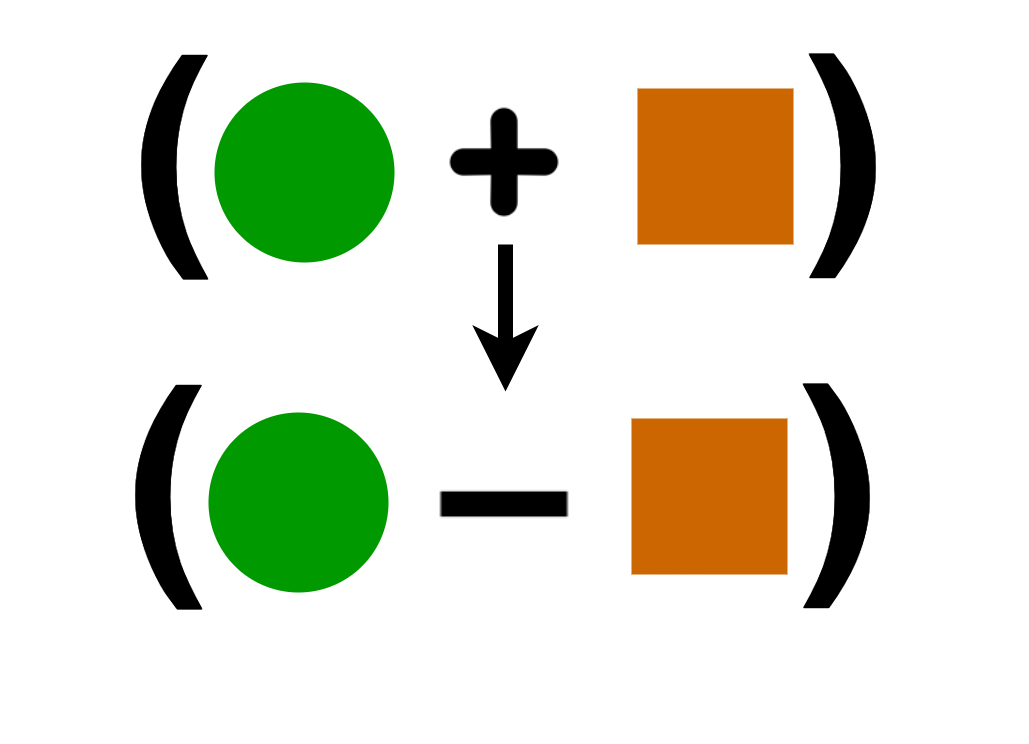 For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(4+sqrt2)`
For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(4+sqrt2)``4/(4-sqrt2)` `=` `4/(4-sqrt2) xx color(crimson)((4+sqrt2)/(4+sqrt2))` `=` `(4 xx 4+4sqrt2)/((4-sqrt2)(4+sqrt2))` Simplify using the difference of two squares `=` `(16+4sqrt2)/(4^2-(sqrt2)^2)` Simplify square roots `=` `(16+4sqrt2)/16-2` `4^2 = 16` and `(sqrt(2))^2 = 2` `=` `(16 color(crimson)(-:2)+4sqrt2 color(crimson)(-:2))/(14 color(crimson)(-:2))` Simplify by dividing throughout by `2` `=` `(8+2sqrt2)/7` `(8+2sqrt2)/7` -
Question 4 of 4
4. Question
Express the following with rational denominators:
`12/(sqrt7-sqrt3)`
Correct
Excellent!
Incorrect
Difference of Two Squares
`(a+b)(a-b)=a^2-b^2`The conjugate is where we change the sign in the middle of two terms like this:
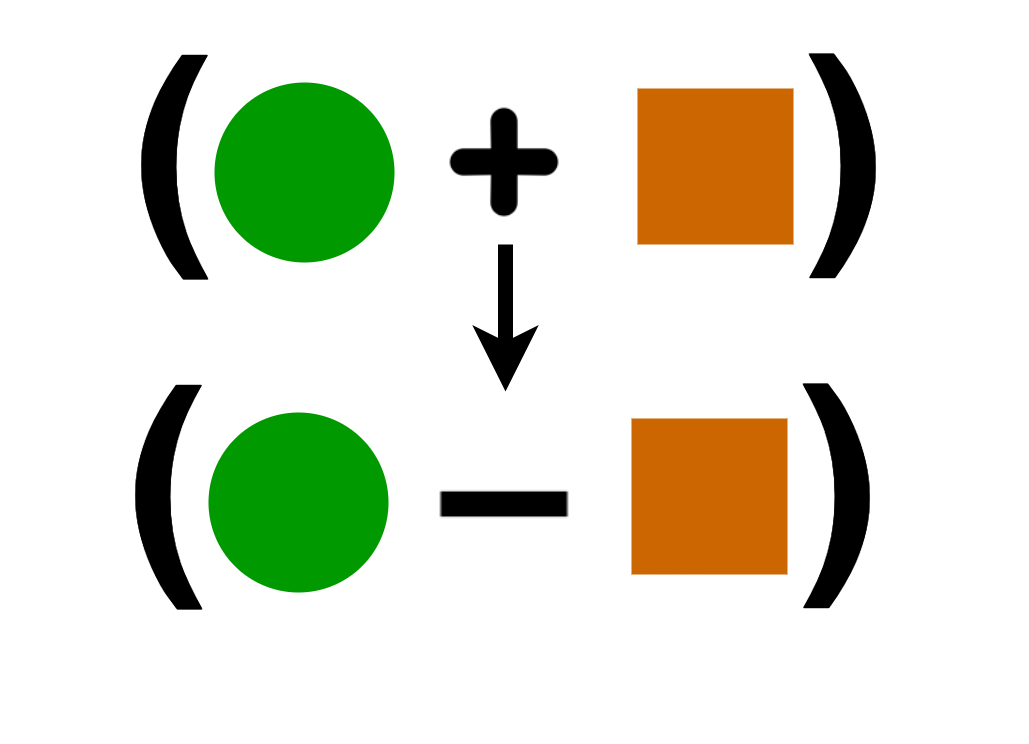 For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(sqrt7+sqrt3)`
For the answer to be in simplest form, the denominator should be a rational number.Multiply the numerator and the denominator by the conjugate of the denominator which is: `color(crimson)(sqrt7+sqrt3)``12/(sqrt7-sqrt3)` `=` `12/(sqrt7-sqrt3) xx color(crimson)((sqrt7+sqrt3)/(sqrt7+sqrt3))` `=` `(12(sqrt7+sqrt3))/((sqrt7-sqrt3)(sqrt7+sqrt3))` Simplify using the difference of two squares `=` `(12(sqrt7+sqrt3))/((sqrt7)^2-(sqrt3)^2)` Simplify square roots `=` `(12(sqrt7+sqrt3))/(7-3)` `(sqrt(7))^2 = 7` and `(sqrt(3))^2 = 3` `=` `(12(sqrt7+sqrt3))/4` `=` `(color(crimson)(4-:)12(sqrt7+sqrt3))/(4color(crimson)(-:4))` Divide top and bottom by `4` `=` `(3(sqrt7+sqrt3))/(class{pk-strike}{4color(crimson)(-:4})` Apply the distributive property `=` `3sqrt7+3sqrt3` `sqrt6+sqrt5`
Quizzes
- Simplify Square Roots 1
- Simplify Square Roots 2
- Simplify Square Roots 3
- Simplify Square Roots 4
- Simplify Radicals with Variables 1
- Simplify Radicals with Variables 2
- Simplify Radicals with Variables 3
- Rewriting Entire and Mixed Radicals 1
- Rewriting Entire and Mixed Radicals 2
- Add and Subtract Radical Expressions (Basic) 1
- Add and Subtract Radical Expressions (Basic) 2
- Add and Subtract Radical Expressions (Basic) 3
- Add and Subtract Radical Expressions 1
- Add and Subtract Radical Expressions 2
- Add and Subtract Radical Expressions 3
- Multiply Radical Expressions 1
- Multiply Radical Expressions 2
- Multiply Radical Expressions 3
- Multiply Radical Expressions 4
- Divide Radical Expressions 1
- Divide Radical Expressions 2
- Divide Radical Expressions 3
- Multiply and Divide Radical Expressions
- Simplify Radical Expressions using the Distributive Property 1
- Simplify Radical Expressions using the Distributive Property 2
- Simplify Radical Expressions using the Distributive Property 3
- Simplify Binomial Radical Expressions using the FOIL Method 1
- Simplify Binomial Radical Expressions using the FOIL Method 2
- Rationalizing the Denominator 1
- Rationalizing the Denominator 2
- Rationalizing the Denominator 3
- Rationalizing the Denominator 4
- Rationalizing the Denominator using Conjugates


